An Improved Fracture Criterion for Mixed-Mode Delamination in Composite Materials

Chen, Xinyuan; Yuan, Chengce; Zhang, Wei; Chen, Weiqiu

doi:10.3389/arc.2025.14365

ORIGINAL RESEARCH

Aerosp. Res. Commun., 28 April 2025

Volume 3 - 2025 | https://doi.org/10.3389/arc.2025.14365

An Improved Fracture Criterion for Mixed-Mode Delamination in Composite Materials

Xinyuan Chen¹

Chengce Yuan²

Wei Zhang^1,3*

Weiqiu Chen^1,4,5*

¹Department of Engineering Mechanics, Zhejiang University, Hangzhou, China
²AVIC Shenyang Aircraft Corporation, Shenyang, China
³System Innovation Center, China, Special Vehicle Research Institute Jingmen, China
⁴Huanjiang Laboratory of Zhejiang University, Zhuji, China
⁵Faculty of Mechanical Engineering and Mechanics, Ningbo University, Ningbo, China

Delamination is a common failure mode in laminated composites, usually under I/II mixed-mode loading. This paper incorporates the influence of mixed-mode ratio on the critical distance in the fracture criterion based on the minimum strain energy density for delamination failure in composites. Meanwhile, the impact of energy dissipation within the fracture process zone on delamination failure is further considered, leading to an I/II mixed-mode delamination fracture criterion applicable to orthotropic composites. With this novel criterion, the theoretical predictions are in good agreement with experimental data for both natural orthotropic materials and artificial laminated composites. Compared with the traditional mixed-mode fracture criteria based on strain energy density, the new criterion can more accurately capture the experimentally observed “overshoot” phenomenon and is closer to the actual failure situation.

Introduction

Laminates composites are well-known for their exceptional mechanical properties, including high specific stiffness, specific strength, and excellent energy absorption capability. Furthermore, their design flexibility has led to the widespread application in various scenarios such as aerospace, automotive, and sports equipment [1–6]. However, laminate composites may suffer from delamination damage even failure within the internal structures when subjected to external loads [7–9]. Due to the heterogeneity of composite materials, simulating mechanical behavior becomes extremely intricate. Consequently, establishing a suitable fracture criterion from a theoretical standpoint to predict the delamination failure of laminated composites is of significant importance [10–12].

Loading under pure mode I, pure mode II, and mixed-mode of type I/II can all contribute to delamination failure in laminated composites. For pure-mode delamination, the fracture criterion can be easily established by comparing the energy release rate (ERR) with its fracture toughness, and the methods for determining pure-mode fracture toughness have been relatively well-developed. However, delamination failure occurs frequently under mixed-mode loading. Unlike pure mode, the failure mechanism of mixed-mode fracture is relatively more complex [8, 12]. Numerous researchers have proposed a variety of fracture criteria to predict the delamination failure of laminated composites under I/II mixed-mode loading [10, 13–15], which typically require experimental determination of certain material parameters. In 1965, Wu et al. [16] proposed a linear fracture criterion and assumed that the ERR contributes linearly to the mixed-mode fracture toughness in pure mode. Some researchers have adopted another approach, utilizing the stress field solution of cracks in orthotropic materials [17, 18] to extend the fracture theories, which are traditionally applied to isotropic materials, to orthotropic composite materials [12, 19–23]. Jernkvist [23] extended several existing isotropic fracture theories, including maximum strain energy release rate [19], minimum strain energy density [22], and traditional maximum shear stress [24], to the orthotropic cases, and established a criterion for predicting the I/II mixed-mode fracture of orthotropic wood. However, comparison with experimental data reveals that the criterion proposed by Jernkvist is conservative. It is because that Jernkvist did not consider the influence of fiber bridging toughening (i.e., the energy dissipated by the fracture process zone), which is now known as the FPZ effect [25].

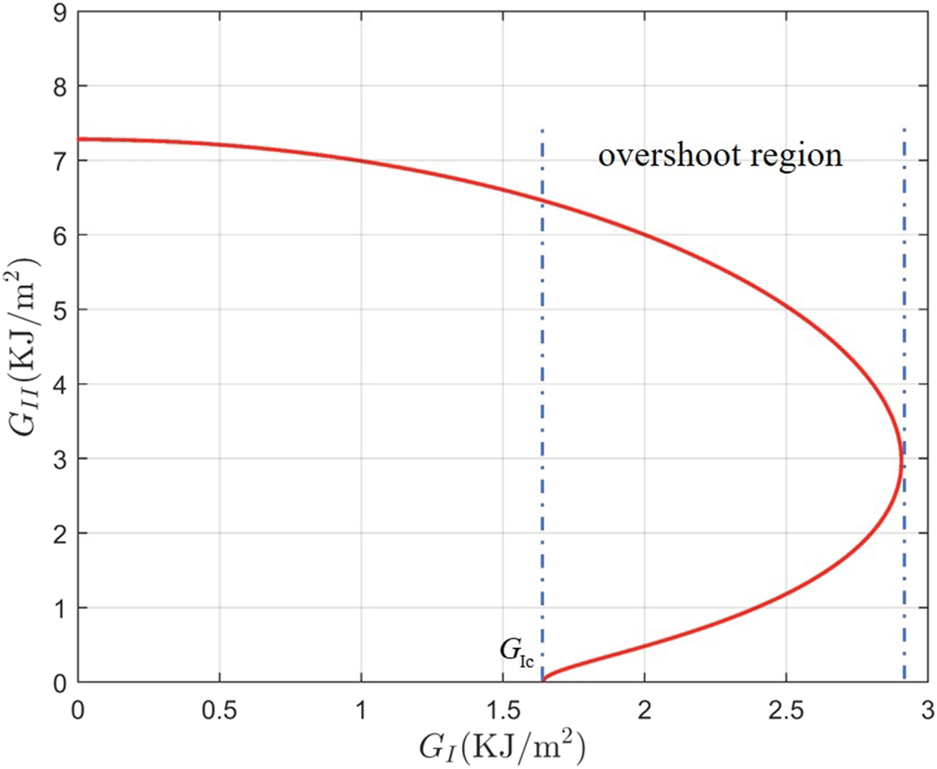
In fact, many researchers have confirmed that the energy dissipated by the fracture process zone (FPZ) has a significant impact on the delamination failure of laminated composites [7, 26–33]. In recent studies, Daneshjoo et al. [25] extended the minimum strain energy density theory to orthotropic materials by considering the energy absorbed by the FPZ and introducing the concept of damage factor, and proposed a new I/II mixed-mode fracture criterion. Mirsayar [31] proposed a stress/energy-based criterion to predict the I/II mixed-mode fracture behavior of laminated composites. This combined criterion considers the FPZ effect by calculating the absorbed energy due to the fiber bridging micromechanism and converting it into a defined effective critical distance, and then calculates the maximum principal stress around the crack tip to predict fracture occurrence. Compared with other criteria, Mirsayar’s criterion shows a higher correlation between the theoretical results and experimental data. Nevertheless, both the criteria proposed by Daneshjoo et al. [25] and Mirsayar [31] cannot capture the unique “overshoot” phenomenon observed in the failure of laminated composites. This “overshoot” phenomenon refers to the fact that under I/II mixed-mode loading, the mode I component $G_{I}$ of the energy release rate will increase and exceed the critical value $G_{IC}$ with the appearance of a certain amount of mode II component $G_{II}$ , and then gradually decrease to zero as the mode II component $G_{II}$ increases, which will result in an “overshoot” region in the predicted curve [12, 34–36], as depicted in Figure 1.

Figure 1

Figure 1. The overshoot phenomenon that has been observed experimentally [12, 34–36].

Recently, Cao et al. [8] improved the traditional fracture criteria, i.e., the maximum principal stress (MPS) criterion [23] and the maximum shear stress (MSS) criterion [37] for orthotropic materials by considering the influence of the mode ratio on the critical distance, leading to the modified maximum principal stress (M-MPS) criterion and the modified maximum shear stress (M-MSS) criterion. The proposed criteria can predict the delamination fracture behavior of laminated composites with relatively high accuracy, and can capture the “overshoot” phenomenon of some materials to a certain extent, but not all materials. To discuss the “overshoot” behavior, Cao et al. [8] proposed a dimensionless parameter characterizing the fracture mechanism, namely, the fracture index, and discussed the dependence of the “overshoot” phenomenon on the fracture index.

From the above literature review, we may conclude that although significant efforts have been made to derive the mixed-mode fracture criteria of composite materials, their ability to predict the fracture failure trend remains somewhat limited. An effective mixed-mode failure criterion that can properly consider the influence of critical distance and FPZ toughening mechanism, and can well capture the overshoot phenomenon, has not been developed yet.

This paper develops an improved minimum strain energy density method for evaluating the delamination behavior of orthotropic composite materials under mixed-mode (I/II) loading. In Section Basic Formulations, we first briefly outline the model of this study (Section A Crack in an Orthotropic Material), and then elaborate on the stress field at the crack tip of orthotropic materials (Section Stress Analysis at the Crack Tip), laying the foundation for subsequent theoretical analysis. In Section Fracture Criteria for Laminated Composites, we review the classical fracture criteria based on stress and strain energy density methods (Section A Brief Review of Classical Fracture Criteria). Subsequently, we introduce the first improvement to the traditional minimum strain energy density method, abandoning the assumption of constant critical distance and considering the influence of mixed-mode ratio on the critical fracture distance (Section The Improved Fracture Criterion). Based on this, we further consider the effect of energy dissipation in the FPZ on delamination failure, and finally obtain an improved fracture criterion using the minimum strain energy density method. In Section Results and Discussion, we apply the new criterion to the prediction of natural orthotropic materials—wood, and artificial laminated composites, and compare it with existing experimental data as well as the mixed-mode fracture criteria based on stress and energy methods, respectively, verifying the accuracy and superiority of the new criterion.

Basic Formulations

A Crack in an Orthotropic Material

As shown in Figure 2, an orthotropic plate containing a sharp notch (or an embedded crack) along the fiber layup direction is subjected to an in-plane loading. We assume that the crack opening stress is non-negative, thereby guaranteeing that the crack surfaces remain open, and the crack will propagate in a self-similar pattern, i.e., the crack will propagate in the original plane without deviation [23, 38].

Figure 2

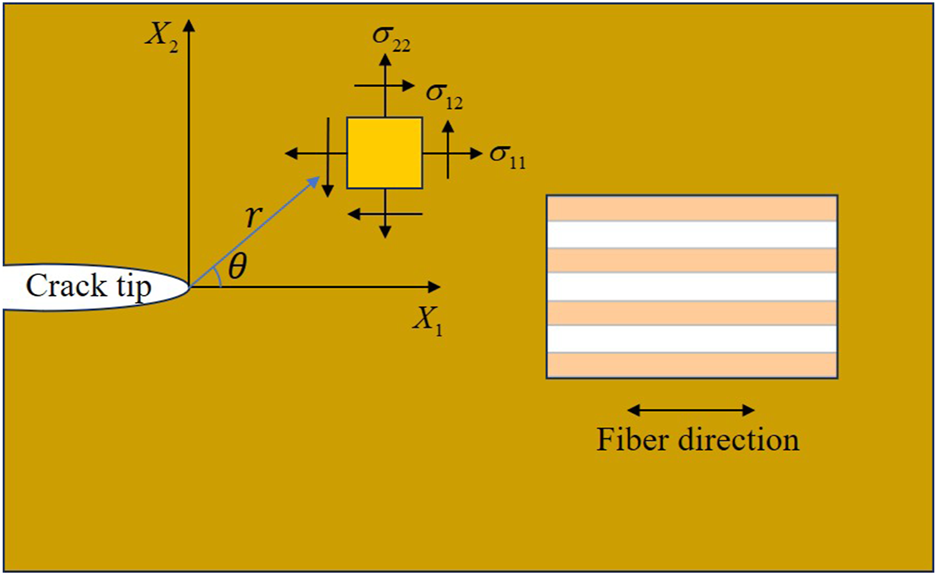
Figure 2. Composite laminate with cracks.

Stress Analysis at the Crack Tip

For a linear elastic orthotropic material, as depicted in Figure 2, we consider a crack that extends and penetrates within the $X_{1} - X_{3}$ plane, that is, the normal of the crack face is parallel to the $X_{2} -$ axis. The stress field around its crack tip can be expressed as [17, 18, 39]:

σ_{i j} = \frac{1}{\sqrt{2 π r}} [K_{I} f_{i j} (θ) + K_{II} g_{i j} (θ)], (i, j = 1, 2) (1)

where the $X_{1} -$ axis of the Cartesian coordinate system is defined along the fiber layup direction, $r$ and $θ$ are the polar coordinates, $K_{I}$ and $K_{II}$ are the stress intensity factors of type I and II induced by the external load, respectively, $f_{i j} (θ)$ and $g_{i j} (θ)$ depend on the material properties of the orthotropic material:

\begin{array}{l} f_{11} (θ) = Re [\frac{x_{1} x_{2} (x_{2} T_{2} - x_{1} T_{1})}{x_{1} - x_{2}}], & g_{11} (θ) = Re [\frac{x_{2}^{2} T_{2} - x_{1}^{2} T_{1}}{x_{1} - x_{2}}] \\ f_{22} (θ) = Re [\frac{x_{1} T_{2} - x_{2} T_{1}}{x_{1} - x_{2}}], & g_{22} (θ) = Re [\frac{T_{2} - T_{1}}{x_{1} - x_{2}}] \\ f_{12} (θ) = Re [\frac{x_{1} x_{2} (T_{1} - T_{2})}{x_{1} - x_{2}}], & g_{12} (θ) = Re [\frac{x_{1} T_{1} - x_{2} T_{2}}{x_{1} - x_{2}}] \end{array} (2)

where

T_{1} = \frac{1}{\sqrt{(\cos θ + x_{1} \sin θ)}}, T_{2} = \frac{1}{\sqrt{(\cos θ + x_{2} \sin θ)}} (3)

$x_{1}$ , ${\bar{x}}_{1}$ and $x_{2}$ , ${\bar{x}}_{2}$ (an overbar indicates the conjugate) are the four roots of the following characteristic equation:

A_{11} x^{4} - 2 A_{16} x^{3} + (2 A_{12} + A_{66}) x^{2} - 2 A_{26} x + A_{22} = 0 (4)

where the coefficients $A_{i j}$ are derived from the constitutive relation:

(\begin{array}{l} ε_{11} \\ ε_{22} \\ ε_{33} \\ γ_{23} \\ γ_{31} \\ γ_{12} \end{array}) = (\begin{array}{c} 1 / E_{1} & - ν_{21} / E_{2} & - ν_{31} / E_{3} & 0 & 0 & 0 \\ - ν_{12} / E_{1} & 1 / E_{2} & - ν_{32} / E_{3} & 0 & 0 & 0 \\ - ν_{13} / E_{1} & - ν_{23} / E_{2} & 1 / E_{3} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 / G_{23} & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 / G_{31} & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 / G_{12} \end{array}) (\begin{array}{l} σ_{11} \\ σ_{22} \\ σ_{33} \\ σ_{23} \\ σ_{31} \\ σ_{12} \end{array}) (5)

For the case of plane-strain, $A_{16} = A_{26} = 0$ and the four flexibility coefficients $A_{i j}$ need to be replaced by $A_{i j}^{'}$ , which are given by

A_{i j}^{'} = A_{i j} - \frac{A_{i 3} A_{j 3}}{A_{33}}, (i, j = 1, 2) (6)

Fracture Criteria for Laminated Composites

A Brief Review of Classical Fracture Criteria

The experimental fracture criteria are derived by fitting the experimental data of fracture toughness under different mixed-mode ratios. While they are good at predicting mixed-mode delamination of composites, extracting the parameters involved in them is time consuming and costly. Due to the limitations of experimental fracture criteria, numerous scholars have been dedicated to the study of theoretical fracture criteria for composites, which are mainly based on stress or energy. Jernkvist [20, 23] proposed the maximum principal stress (MPS) criterion, the maximum strain energy release rate (MSERR) criterion, and the minimum strain energy density (MSED) criterion for composite materials, based on the assumption that delamination extends along the fiber direction. Fakoor and Rafiee also proposed a fracture criterion for composite materials based on the maximum shear stress (MSS) [37]. Cao et al. [8] further proposed the modified maximum principal stress (M-MPS) criterion and the modified maximum shear stress (M-MSS) criterion in consideration of the influence of mode ratio on the critical distance. Similarly, Daneshjoo et al. [25] proposed a fracture criterion based on the MSED method, which takes account of the toughening effect of the fracture process zone (FPZ) by introducing a damage factor associated with the fiber bridging effect.

Stress-Based Fracture Criteria

It is easy to see that the MPS around the crack tip shown in Figure 2 is:

σ_{\max} = (\frac{σ_{11} + σ_{22}}{2}) + \sqrt{{(\frac{σ_{11} - σ_{22}}{2})}^{2} + σ_{12}^{2}} (7)

Assume that the crack extends in a self-similar manner along the fiber direction ( $θ = 0$ ). Substituting Equation 1 into Equation 7, gives:

σ_{\max} = \frac{1}{\sqrt{2 π r^{p}}} (β_{1} K_{I} + \sqrt{β_{2} {K_{I}}^{2} + {K_{II}}^{2}}) (8)

where $β_{1} = \frac{f_{11} (0) + f_{22} (0)}{2}, β_{2} = {[\frac{f_{11} (0) - f_{22} (0)}{2}]}^{2}$ .

According to the MPS criterion, when $r^{p}$ reaches the critical distance $r_{c}^{p}$ , the MPS $σ_{\max}$ reaches the critical value $σ_{cr}$ , and the material will fracture, regardless of the loading type (I or II). Within the framework of linear elastic fracture mechanics without considering the fiber bridging effect, the critical distance $r_{c}^{p}$ mainly depends on the fracture toughness and strength of the material [23, 25, 37].

Thus, the MPS fracture criterion for orthotropic materials is obtained as follows [23]:

(β_{1} K_{I} + \sqrt{β_{2} {K_{I}}^{2} + {K_{II}}^{2}}) - (β_{1} + \sqrt{β_{2}}) K_{Ic} = 0 (9)

Similarly, the MSS near the crack tip can be expressed as:

τ_{\max} = \sqrt{{(\frac{σ_{11} - σ_{22}}{2})}^{2} + σ_{12}^{2}} (10)

Setting $θ = 0$ , and substituting Equation 1 into Equation 10, we obtain:

τ_{\max} = \frac{1}{\sqrt{2 π r^{s}}} (\sqrt{β_{2} {K_{I}}^{2} + {K_{II}}^{2}}) (11)

Similarly, according to the MSS criterion, when $r^{s}$ reaches the critical distance $r_{c}^{s}$ , the MSS $τ_{\max}$ reaches the critical value $τ_{cr}$ , and either type I or II loading will result in fracture. Therefore, the MSS fracture criterion for orthotropic materials is obtained as follows [37]:

β_{2} {K_{I}}^{2} + {K_{II}}^{2} - β_{2} {K_{Ic}}^{2} = 0 (12)

It can be seen from above that the traditional MPS criterion and MSS criterion for orthotropic materials fail to take into account the influence of mode ratio on fracture. In contrast, the M-MPS criterion and M-MSS criterion are derived by considering the influence of mode ratio on the critical distance [8].

Assuming that $r_{c}$ depends on the mode ratio, and replacing $r^{p}$ in Equation 8 with $r^{p} (2 ψ)$ , leads to:

σ_{\max} = \frac{1}{\sqrt{2 π r^{p} (2 ψ)}} (β_{1} K_{I} + \sqrt{β_{2} {K_{I}}^{2} + {K_{II}}^{2}}) (13)

where $ψ$ is the mode mixing angle, whose value is determined by $K_{I}$ and $K_{II}$ [8].

Following a similar derivation process to the MPS criterion, we can obtain the M-MPS criterion applicable to orthotropic materials as

β_{1} K_{I} + \sqrt{β_{2} {K_{I}}^{2} + {K_{II}}^{2}} = \sqrt{\frac{1}{\frac{1}{{(β_{1} + \sqrt{β_{2}})}^{2} {K_{Ic}}^{2}} \cos^{2} (2 ψ) + \frac{1}{{K_{IIc}}^{2}} \sin^{2} (2 ψ)}} (14)

Similarly, the M-MSS criterion can be derived as

β_{2} {K_{I}}^{2} + {K_{II}}^{2} = \frac{1}{\frac{1}{β_{2} {K_{Ic}}^{2}} \cos^{2} (2 ψ) + \frac{1}{{K_{IIc}}^{2}} \sin^{2} (2 ψ)} (15)

For more details, the reader is referred to Ref. [8].

Energy Based Fracture Criterion

Sih [22] proposed that crack propagation may be predicted based on the local strain energy density at the crack tip. For a linear elastic orthotropic material as shown in Figure 2, the strain energy density $w$ around the crack tip is expressed as

w = \frac{1}{2} σ_{i j} ε_{i j} (16)

Under the plane-strain assumption, substituting the relation in Equation 5 into Equation 16 gives the following expression for the strain energy density:

w = \frac{A_{11}^{'}}{2} σ_{11}^{2} + \frac{A_{22}^{'}}{2} σ_{22}^{2} + A_{12}^{'} σ_{11} σ_{22} + \frac{A_{66}^{'}}{2} σ_{12}^{2} (17)

Substituting the stress field near the crack tip in Equation 1 into Equation 17 yields:

w = K_{I}^{2} B_{1} (r, θ) + K_{II}^{2} B_{2} (r, θ) + 2 K_{I} K_{II} B_{3} (r, θ) (18)

where $B_{i} (i = 1, 2, 3)$ are complex functions of $r$ and $θ$ , involving the orthotropic material constants, as:

\begin{array}{l} B_{1} (r, θ) = \frac{1}{r} [\frac{A_{11}^{'}}{4 π} f_{11}^{2} (θ) + \frac{A_{22}^{'}}{4 π} f_{22}^{2} (θ) + \frac{A_{12}^{'}}{2 π} f_{11} (θ) f_{22} (θ) + \frac{A_{66}^{'}}{4 π} f_{12}^{2} (θ)] \equiv \frac{1}{r} D_{1} (θ) \\ B_{2} (r, θ) = \frac{1}{r} [\frac{A_{11}^{'}}{4 π} g_{11}^{2} (θ) + \frac{A_{22}^{'}}{4 π} g_{22}^{2} (θ) + \frac{A_{12}^{'}}{2 π} g_{11} (θ) g_{22} (θ) + \frac{A_{66}^{'}}{4 π} g_{12}^{2} (θ)] \equiv \frac{1}{r} D_{2} (θ) \\ B_{3} (r, θ) = \frac{1}{r} \{\frac{A_{11}^{'}}{4 π} f_{11} (θ) g_{11} (θ) + \frac{A_{22}^{'}}{4 π} f_{22} (θ) g_{22} (θ) + \frac{A_{12}^{'}}{4 π} [f_{11} (θ) g_{22} (θ) + f_{22} (θ) g_{11} (θ)] + \frac{A_{66}^{'}}{4 π} f_{12} (θ) g_{12} (θ)} \\ \equiv \frac{1}{r} D_{3} (θ) \end{array} (19)

The MSED theory states that:

(1) The crack propagates along the direction given by the local minimum $w$ of the angular coordinate $θ$ in Figure 2, under mixed-mode (I/II) loading:

\frac{\partial w}{\partial θ} = 0 and \frac{\partial^{2} w}{\partial θ^{2}} > 0, at θ = θ_{0} (20)

(2) When the strain energy density $w$ reaches a critical value $w_{c}$ at a certain distance $r_{c}$ from the crack tip in the direction of $θ = θ_{0}$ , the crack propagates.

It is important to emphasize that unlike the first point in the MSED theory, we employ here an assumption similar to the stress method as mentioned earlier, which assumes that the crack extends along the fiber direction in a self-similar manner, i.e., $θ_{0} = 0$ . In Sih’s analysis, it is also assumed that the critical distance $r_{c} = δ$ . Then, we have:

w (r = δ, θ = 0) = \frac{A_{66}^{'} g_{12}^{2} (0)}{4 π δ} (ρ K_{I}^{2} + K_{II}^{2}) = w_{c} (21)

where

ρ = \frac{A_{11}^{'} f_{11}^{2} (0) + A_{22}^{'} f_{22}^{2} (0) + 2 A_{12}^{'} f_{11} (0) f_{22} (0)}{A_{66}^{'} g_{12}^{2} (0)} (22)

Equation 21 should be valid for both pure type I loading and pure type II loading. Thus, the following relationship between type I fracture toughness and type II fracture toughness can be obtained:

\frac{K_{IIc}}{K_{Ic}} = \sqrt{ρ} (23)

Using the relationship in Equation 21, the mixed-mode fracture criterion in terms of stress intensity factors of type I/II can be derived as:

K_{I}^{2} + \frac{1}{ρ} K_{II}^{2} - K_{Ic}^{2} = 0 (24)

Based on this, Daneshjoo et al. [25] considered the case of crack initiation angle $θ_{0} \neq 0$ by defining a suitable damage factor, and further took into account the energy absorbed in the FPZ. A new fracture criterion is thus proposed as:

K_{I}^{2} + \frac{1}{α} K_{II}^{2} = K_{Ic}^{2} (25)

where

α = \frac{B_{1} (δ, θ_{0 I})}{B_{2} (δ, θ_{0 II})} - \frac{B_{1} (δ, θ_{0 I})}{B_{2} (δ, θ_{0 II})} {(\frac{K_{FPZI}}{K_{Ic}})}^{2} + {(\frac{K_{FPZII}}{K_{Ic}})}^{2} (26)

where $θ_{0 I}$ and $θ_{0 II}$ are the crack initiation angles under pure type I loading and pure type II loading respectively, which can be calculated by Equation 20. That equation is nonlinear and complex, and it is theoretically difficult to obtain the analytical solution of $θ_{0 I}$ or $θ_{0 II}$ . In Daneshjoo et al. [25], the solutions of $θ_{0 I}$ and $θ_{0 II}$ are obtained numerically with the given set of material properties. $K_{FPZI}$ and $K_{FPZII}$ in Equation 26 are the type I and type II stress intensity factors in the FPZ, respectively.

The Improved Fracture Criterion

As can be seen from the discussions in the previous sub-section, traditional and recent fracture criteria based on the strain energy density generally do not consider the influence of mode ratio on the critical distance $r_{c}$ for crack propagation. However, the study of Cao et al. [8] shows that fracture damage in orthotropic materials exhibits significant difference when the mode ratio changes. Therefore, this study will incorporate the influence of mode ratio on the critical distance $r_{c}$ into the strain energy density method. To this end, we suggest the following modifications to the expression for critical strain energy density:

w_{c} = \frac{1}{r_{c} (φ)} [K_{I}^{2} D_{1} (θ_{0}) + K_{II}^{2} D_{2} (θ_{0}) + 2 K_{I} K_{II} D_{3} (θ_{0})] (27)

where $D_{i} (θ_{0}) (i = 1, 2, 3)$ are defined in Equation 19. $φ$ is defined as the mixed-mode angle, which is determined by $K_{I}$ and $K_{II}$ , that is $φ = \arctan (\frac{K_{II}}{\sqrt{β_{2}} K_{I}})$ , $0 \leq φ \leq \frac{π}{2}$ , $β_{2} = {[\frac{f_{11} (0) - f_{22} (0)}{2}]}^{2}$ .

Consider that the crack extends in a self-similar manner along the fiber direction ( $θ_{0} = 0$ ). Then, Equation 27 takes the following forms for pure mode I and pure mode II fracture:

\begin{array}{l} Pure Mode I \to w = \frac{1}{r_{Ic}} K_{Ic}^{2} D_{1} (0) = w_{c} \\ Pure Mode II \to w = \frac{1}{r_{IIc}} K_{IIc}^{2} D_{2} (0) = w_{c} \end{array} (28)

where $r_{Ic}$ and $r_{IIc}$ are the critical distances for pure mode I and pure mode II fracture, respectively. It is difficult to determine the critical distance $r_{c} (φ)$ either experimentally or theoretically. Following Cao et al. [8], we adopt the following expression for estimation:

\frac{1}{r_{c} (φ)} = \frac{1}{r_{Ic}} \cos^{2} (φ) + \frac{1}{r_{IIc}} \sin^{2} (φ) (29)

Equation 29 should be applicable to both pure mode I and pure mode II fracture. From Equation 28, we can obtain:

\frac{r_{IIc}}{r_{Ic}} = \frac{K_{IIc}^{2} D_{2} (0)}{K_{Ic}^{2} D_{1} (0)} (30)

Furthermore, the following relationship holds under any mixed mode ratio:

\begin{array}{l} w_{c} (Any mode ratio) = \frac{1}{r_{c} (φ)} [K_{I}^{2} D_{1} (0) + K_{II}^{2} D_{2} (0) + 2 K_{I} K_{II} D_{3} (0)] \\ = [\frac{1}{r_{Ic}} \cos^{2} (φ) + \frac{1}{r_{IIc}} \sin^{2} (φ)] \times [K_{I}^{2} D_{1} (0) + K_{II}^{2} D_{2} (0) + 2 K_{I} K_{II} D_{3} (0)] \\ = w_{c} (Pure Mode I) = \frac{1}{r_{Ic}} K_{Ic}^{2} D_{1} (0) \end{array} (31)

Substituting Equation 30 into the above equation, we obtain after simplification the mixed fracture criterion based on the strain energy density method, with the influence of mode ratio on the critical distance $r_{c}$ :

D_{1} (0) K_{I}^{2} + D_{2} (0) K_{II}^{2} + 2 D_{3} (0) K_{I} K_{II} = \frac{1}{\frac{\cos^{2} (φ)}{D_{1} (0) K_{Ic}^{2}} + \frac{\sin^{2} (φ)}{D_{2} (0) K_{IIc}^{2}}} (32)

In the derivation above, we treat the critical strain energy density $w_{c}$ as an intrinsic material property and assume that all the energy induced by loading confronts this property, regardless of the loading mode. However, in the case of delamination failure in composite materials subjected to mixed mode I/II loading, an FPZ forms near the delamination crack tip, which absorbs energy to delay the fracture. Therefore, to incorporate the influence of FPZ on fracture and establish a more accurate fracture criterion, we introduce the strain energy density term $w_{F}$ of the FPZ, as follows:

\begin{array}{l} w = \frac{1}{r_{c} (φ)} [K_{I}^{2} D_{1} (0) + K_{II}^{2} D_{2} (0) + 2 K_{I} K_{II} D_{3} (0)] \\ = [\frac{1}{r_{Ic}} \cos^{2} (φ) + \frac{1}{r_{IIc}} \sin^{2} (φ)] \times [K_{I}^{2} D_{1} (0) + K_{II}^{2} D_{2} (0) + 2 K_{I} K_{II} D_{3} (0)] \\ = w_{c} + w_{F} \end{array} (33)

Similarly, for pure mode I fracture and pure mode II fracture, Equation 33 takes the following form:

\begin{array}{l} Pure Mode I \to w = \frac{1}{r_{Ic}} K_{Ic}^{2} D_{1} (0) = w_{c} + w_{FI} \\ Pure Mode II \to w = \frac{1}{r_{IIc}} K_{IIc}^{2} D_{2} (0) = w_{c} + w_{FII} \end{array} (34)

where $w_{FI}$ and $w_{FII}$ represent the strain energy density of FPZ in pure mode I and pure mode II fracture, respectively, given by

\begin{array}{l} w_{FI} = \frac{D_{1} (0)}{r_{Ic}} K_{FI}^{2} \\ w_{FII} = \frac{D_{2} (0)}{r_{IIc}} K_{FII}^{2} \end{array} (35)

where $K_{FI}$ and $K_{FII}$ represent the type I and type II stress intensity factors at the FPZ, respectively. The energy of the FPZ is considered to be the energy absorbed by fiber bridging and microcracks, which is released through crack extension [25]. Therefore, the relationship between the stress intensity factor and strain energy release rate for orthotropic materials under the plane-strain condition can be used [17], which states:

K_{FI} = \sqrt{E_{I}^{'} G_{FI}}, K_{FII} = \sqrt{E_{II}^{'} G_{FII}} (36)

where $G_{FI}$ and $G_{FII}$ represent the type I and type II strain energy release rates at the FPZ, respectively. $E_{I}^{'}$ and $E_{II}^{'}$ are the generalized elastic moduli, defined as [17, 25]:

\begin{array}{l} E_{I}^{'} = {[\frac{{A^{'}}_{11} {A^{'}}_{22}}{2} (\sqrt{\frac{{A^{'}}_{22}}{{A_{11}}^{'}}} + \frac{2 {A^{'}}_{12} + {A^{'}}_{66}}{2 {A_{11}}^{'}})]}^{- \frac{1}{2}} \\ E_{II}^{'} = {[\frac{{A^{'}}_{11}^{2}}{2} (\sqrt{\frac{{A^{'}}_{22}}{{A^{'}}_{11}}} + \frac{2 {A^{'}}_{12} + {A^{'}}_{66}}{2 {A^{'}}_{11}})]}^{- \frac{1}{2}} \end{array} (37)

Due to the complexity of obtaining the strain energy at fracture of FPZ under any load mode [26], there is no analytical solution available in the literature. Here we introduce an approximate estimation similar to Equation 29 as:

w_{F} = \frac{D_{1} (0) K_{FI}^{2}}{r_{Ic}} \cos^{2} (φ) + \frac{D_{2} (0) K_{FII}^{2}}{r_{IIc}} \sin^{2} (φ) (38)

By combining Equations 33, 34, 38, we obtain a mixed-mode fracture criterion based on the strain energy density method that comprehensively considers both the influence of the mode ratio on the critical distance and the energy absorption in the FPZ:

D_{1} (0) K_{I}^{2} + D_{2} (0) K_{II}^{2} + 2 D_{3} (0) K_{I} K_{II} = \frac{K_{Ic}^{2} K_{IIc}^{2} - K_{Ic}^{2} K_{FII}^{2} \cos^{2} (φ) - K_{IIc}^{2} K_{FI}^{2} \sin^{2} (φ)}{\frac{\cos^{2} (φ) (K_{IIc}^{2} - K_{FII}^{2})}{D_{1} (0)} + \frac{\sin^{2} (φ) (K_{Ic}^{2} - K_{FI}^{2})}{D_{2} (0)}} (39)

It is evident that both the mixed fracture criteria proposed in the present study, i.e., Equations 32, 39, satisfy the energy constraint conditions for pure mode I fracture and pure mode II fracture. If the influence of the FPZ is ignored, Equation 39 will be simplified to Equation 32.

Results and Discussion

Existing Experimental Cases

To validate the effectiveness and accuracy of the two new I/II mixed-mode fracture criteria (i.e., Equations 32, 39), we collect five sets of material data commonly used for fracture criterion validation. These data encompass the I/II mixed-mode fracture characteristics of natural wood and artificial laminated composites [20, 23, 40]. The basic performance or material parameters of these materials are summarized in Table 1, which provides the necessary information to extract the coefficients required in Equation 32. As for the validation of Equation 39, two additional parameters are needed, namely, the values of energy $G_{F}$ absorbed by the material in the FPZ under pure I-type and pure II-type modes. Table 2 supplements the relevant parameters of five sets of materials [25, 40–49]. Next, we will compare the newly proposed fracture criteria with the stress-based and strain energy density-based fracture criteria discussed in Section Fracture Criteria for Laminated Composites.

Table 1

Table 1. Material properties of orthotropic materials, obtained from Refs [20, 23, 40].

Table 2

Table 2. Supplementary material parameters, obtained from Refs [25, 40–49].

Comparison and Discussion

Comparative analysis mainly includes the following two parts:

(A) Comparison with fracture criteria based on the stress method. We will compare our criteria with the modified fracture criteria proposed by Cao et al. [8], namely M-MPS (Equation 14) and M-MSS (Equation 15).

(B) Comparison with fracture criteria based on the strain energy density (SED) method. We will make a comparison with the traditional strain energy density criterion proposed by Sih [22] (Equation 24) and the one considering the influence of the FPZ proposed by Daneshjoo et al. [25] (Equation 25).

By comparing different fracture criteria with the experimental results for orthotropic composite materials reported in the literature, we are able to validate the newly proposed fracture criteria (Equations 32, 39), as to be discussed in depth in the following.

The first set of experimental data comes from wood, namely, Norway spruce and Scots pine, with the three orthogonal principal axes being in the radial, tangential, and longitudinal directions, respectively. Jernkvist [23] provided a set of experimental data for the mixed I/II type fracture toughness for these two types of wood, which were obtained by testing specimens with cracks along the wood fiber direction. The comparisons with different stress-based fracture criteria and SED-based fracture criteria are shown in Figures 3, 4, respectively.

Figure 3

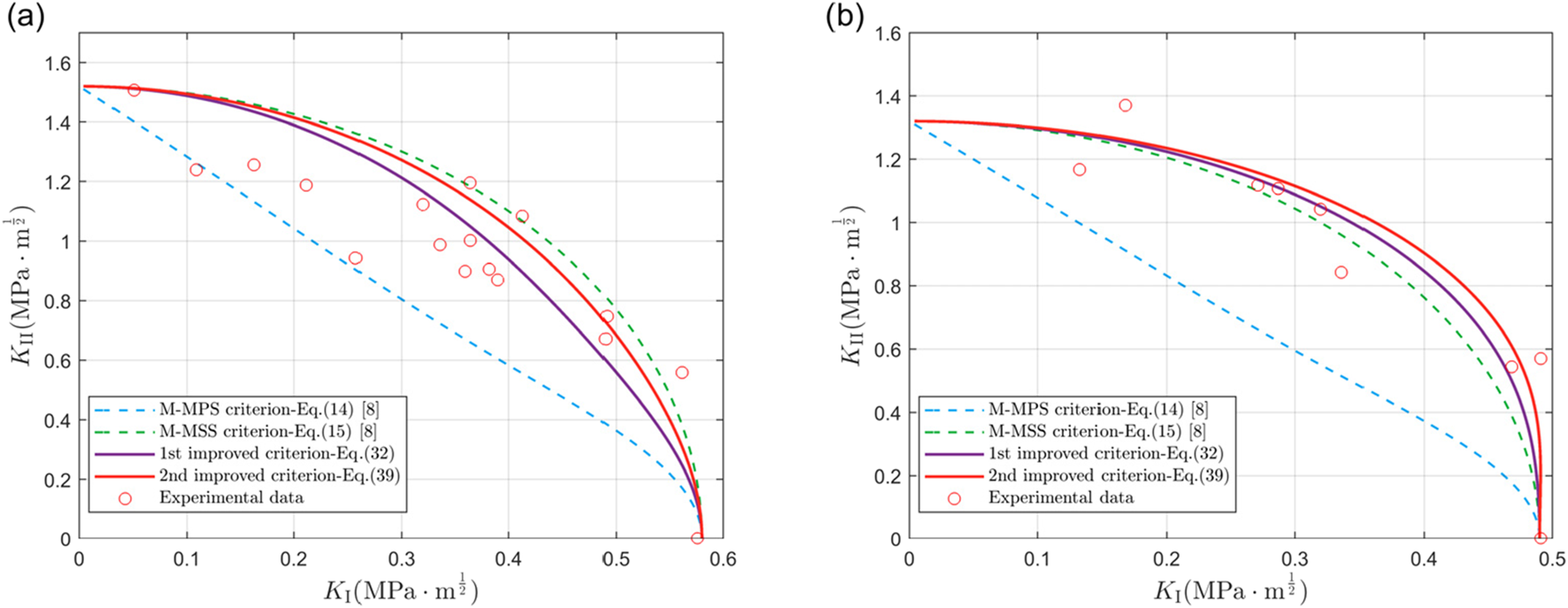
Figure 3. Comparison between our fracture criteria and different stress-based fracture criteria. Experimental data from Refs. [20, 23] are also presented. (a) Norway spruce; (b) Scots pine.

Figure 4

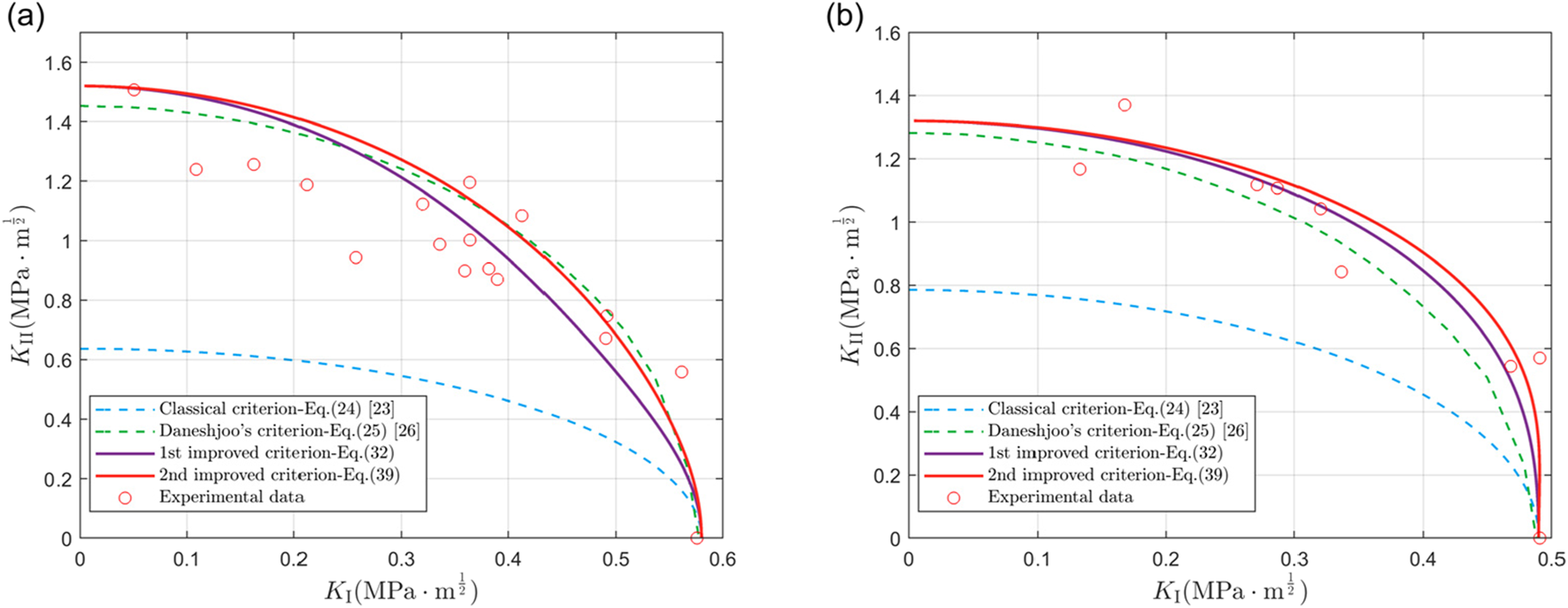
Figure 4. Comparison between our fracture criteria and different SED-based fracture criteria. Experimental data from Refs. [20, 23] are also presented. (a) Norway spruce; (b) Scots pine.

The results show that the two newly proposed fracture criteria (Equations 32, 39) provide the most accurate fracture curves for both types of wood. In contrast, the M-MSS fracture criterion based on the stress method presents a slight deviation, while the M-MPS fracture criterion predicts a significant conservative bias. In the fracture criteria based on the SED method, the traditional fracture criterion (Equation 24) predicts a very conservative curve, while that with the FPZ effect (Equation 25) also shows a slight deviation. These findings further confirm the effectiveness and accuracy of the newly proposed fracture criteria in predicting the fracture behavior of orthotropic composite materials.

The second set of experimental data is from the mixed-mode delamination experiments conducted by Reeder [40] on three unidirectional laminated composite systems: IM7/977-2 carbon fiber/epoxy composite, AS4/3501-6 carbon fiber/epoxy composite, and AS4/PEEK graphite fiber/thermoplastic composite. The energy absorbed by the FPZ involved in these experiments is provided by Ref. [40], see Table 2. Figures 5, 6 show the comparisons of these experimental results with different stress-based fracture criteria and SED based fracture criteria, respectively.

Figure 5

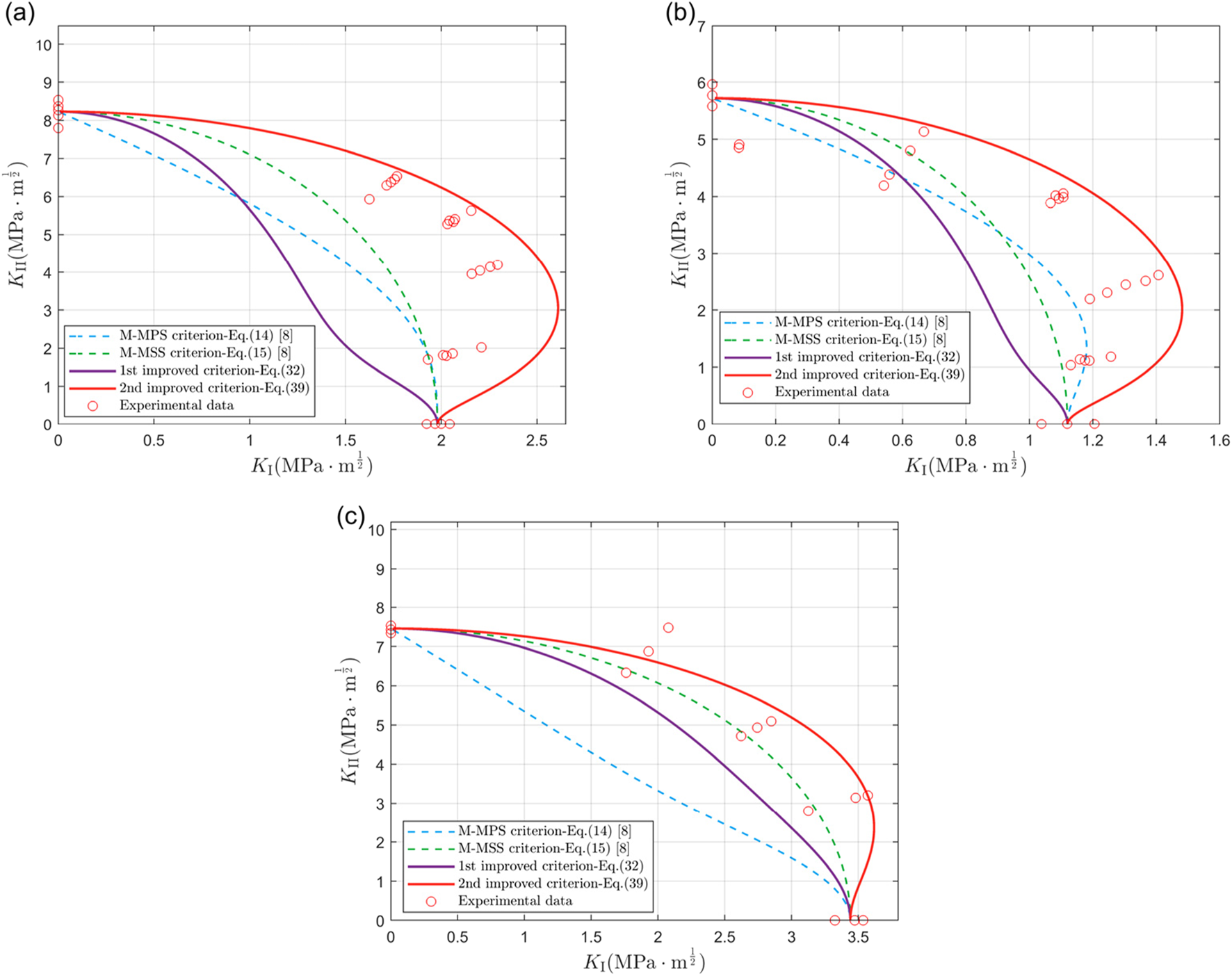
Figure 5. Comparison between our fracture criteria and different stress-based fracture criteria. Experimental data from Ref. [40] are also presented. (a) IM7/977-2; (b) AS4/3501-6; (c) AS4/PEEK.

Figure 6

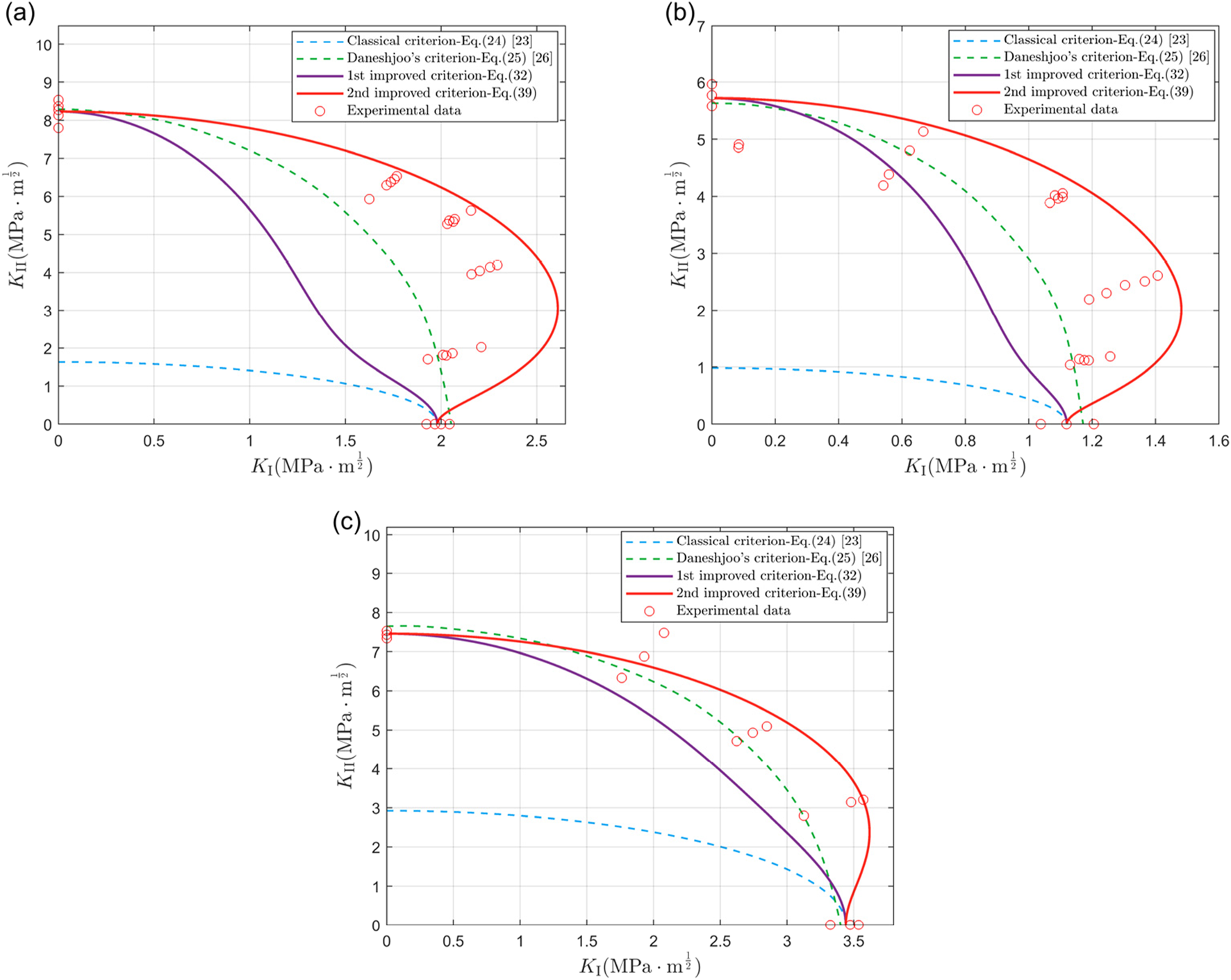
Figure 6. Comparison between our fracture criteria and different SED-based fracture criteria. Experimental data from Ref. [40] are also presented. (a) IM7/977-2; (b) AS4/3501-6; (c) AS4/PEEK.

The comparative results indicate that the novel fracture criterion proposed in Equation 39 provides the most accurate fracture curve. In contrast, the M-MPS criterion (Equation 14), the M-MSS criterion (Equation 15), and the criterion with the FPZ effect (Equation 25) all exhibit conservative trend in predicting the fracture behavior of IM7/977-2 composite materials or AS4/3501-6 composite materials. Especially, the M-MPS criterion (Equation 14) is overly conservative in predicting the fracture of AS4/PEEK composite materials. Meanwhile, the M-MSS criterion (Equation 15) and the criterion with the FPZ effect (Equation 25) are relatively accurate when predicting the fracture performance of AS4/PEEK composite materials.

Furthermore, it is evident from Figure 6 that the traditional SED criterion (Equation 24) is overly conservative in predicting the fracture behavior of these three composite materials, especially when mode II dominates. The improved fracture criterion in Equation 32 considers the influence of mixed-mode ratio on the critical distance, resulting in a significant improvement in prediction accuracy, but it remains conservative. This is just because the first improved criterion (Equation 32) does not account for the energy absorbed by fiber bridging during the fracture process of the composite material, i.e., the energy dissipated in the FPZ. The second improved criterion (Equation 39) that considers the FPZ effect provides a prediction closer to the actual mixed-mode fracture behavior of the composite material.

It is noteworthy that all three composite materials displayed in Figures 5, 6 exhibit an “overshoot” phenomenon in the mixed-mode fracture, i.e., when Mode I dominates, the Mode I component $K_{I}$ of the stress intensity factor significantly exceeds its critical value $K_{Ic}$ . This phenomenon is particularly pronounced in IM7/977-2 and AS4/3501-6 composites. Cao et al. [8] introduced the concept of fracture index and pointed out that the “overshoot” phenomenon is strongly correlated with the fracture index, which becomes more pronounced as the fracture index increases. However, the specific intrinsic mechanism of the “overshoot” phenomenon still needs further investigation. Obviously, among the existing criteria, only the M-MPS criterion (Equation 14) can slightly capture the “overshoot” phenomenon of AS4/3501-6 composite. While the newly proposed improved criterion (Equation 39) can effectively capture the “overshoot” phenomenon of all three materials.

Conclusion

This article proposes a mixed I/II type delamination fracture criterion suitable for orthotropic composite materials, which is based on the minimum strain energy density method. We abandon the assumption of constant critical distance in the traditional method and instead consider the influence of the mixed mode ratio on the critical distance at the time of fracture. Based on this first improvement, the second improvement further abandons the traditional view that the energy absorbed by the composite material during delamination fracture is completely used for delamination extension. We therefore incorporate the influence of the energy dissipated in the fracture process zone (FPZ) into delamination fracture analysis. Compared with the previously proposed mixed-mode fracture criteria, the main advantage of this improvement is that it takes into account the situation that are more aligned with real-world scenarios, providing predictive results that are closer to the actual fracture behavior of composite materials.

By applying the newly proposed criteria to natural orthotropic materials (wood) and artificial laminated composites, and comparing them with the existing experimental data and the mixed-mode fracture criteria based on stress and energy methods, we find that the predictions of the second improved criterion agree well with the experimental data, and can effectively capture the “overshoot” phenomenon, thus verifying the advantages and accuracy of this new criterion.

Despite the success of the criterion in Equation 39 as mentioned above, there are still many uncertainties in the delamination failure of composites, and this newly proposed criterion needs to be validated in a wider range of experiments. Further research is especially necessary on the intrinsic mechanism of delamination failure of composite materials, so that the effects of fracture critical distance, FPZ, crack initiation angle, etc. all can be considered more accurately and realistically.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

XC: Conceptualization, writing – original draft, writing – review and editing. CY: Writing – review and editing. WZ: Writing – review and editing. WC: Supervision, conceptualization, writing – review and editing, funding acquisition. All authors contributed to the article and approved the submitted version.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The work was supported by the National Natural Science Foundation of China (Nos. 12192211 and 12192210), and the 111 Project, PR China (No. B21034). This work was also partly supported by the specialized research projects of Huanjiang Laboratory, Zhuji, Zhejiang Province.

Conflict of Interest

Author CY was employed by the company AVIC Shenyang Aircraft Corporation.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI Statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

References

1. An, H, Youn, BD, and Kim, HS. Reliability-Based Design Optimization of Laminated Composite Structures under Delamination and Material Property Uncertainties. Int J Mech Sci (2021) 205:106561. doi:10.1016/j.ijmecsci.2021.106561

CrossRef Full Text | Google Scholar

2. Gholami, M, Fathi, A, and Baghestani, AM. Multi-Objective Optimal Structural Design of Composite Superstructure Using a Novel MONMPSO Algorithm. Int J Mech Sci (2021) 193:106149. doi:10.1016/j.ijmecsci.2020.106149

CrossRef Full Text | Google Scholar

3. Zheng, X, Sun, Y, Huang, M, An, D, Li, P, Wang, B, et al. Symplectic Superposition Method-Based New Analytic Bending Solutions of Cylindrical Shell Panels. Int J Mech Sci (2019) 152:432–42. doi:10.1016/j.ijmecsci.2019.01.012

CrossRef Full Text | Google Scholar

4. Li, X, Li, YH, and Xie, TF. Vibration Characteristics of a Rotating Composite Laminated Cylindrical Shell in Subsonic Air Flow and Hygrothermal Environment. Int J Mech Sci (2019) 150:356–68. doi:10.1016/j.ijmecsci.2018.10.024

CrossRef Full Text | Google Scholar

5. Banerjee, JR, and Su, H. Dynamic Stiffness Formulation and Free Vibration Analysis of a Spinning Composite Beam. Comput Struct (2006) 84(19):1208–14. doi:10.1016/j.compstruc.2006.01.023

CrossRef Full Text | Google Scholar

6. Zhao, Z, Shen, X, Su, Y, and Chen, W. State-Space Approaches to Complex Structures in Aerospace. Aerosp Res Commun (2023) 1:12394. doi:10.3389/arc.2023.12394

CrossRef Full Text | Google Scholar

7. Fakoor, M, and Khansari, NM. Mixed Mode I/II Fracture Criterion for Orthotropic Materials Based on Damage Zone Properties. Eng Fract Mech (2016) 153:407–20. doi:10.1016/j.engfracmech.2015.11.018

CrossRef Full Text | Google Scholar

8. Cao, T, Gong, Y, Zhao, L, Wang, L, and Hu, N. Stress Based Fracture Criteria for Mixed-Mode I/II Delamination of Unidirectional Composite Laminates. Comput Struct (2024) 344:118325. doi:10.1016/j.compstruct.2024.118325

CrossRef Full Text | Google Scholar

9. Khaji, Z, and Fakoor, M. Examining the Effect of Crack Initiation Angle on Fracture Behavior of Orthotropic Materials under Mixed-Mode I/II Loading. Int J Sol Struct. (2022) 256:111952. doi:10.1016/j.ijsolstr.2022.111952

CrossRef Full Text | Google Scholar

10. Pascoe, JA, Alderliesten, RC, and Benedictus, R. Methods for the Prediction of Fatigue Delamination Growth in Composites and Adhesive Bonds – A Critical Review. Eng Fract Mech (2013) 112–113:72–96. doi:10.1016/j.engfracmech.2013.10.003

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Jamali, J, Mahmoodi, MJ, Hassanzadeh-Aghdam, MK, and Wood, JT. A Mechanistic Criterion for the Mixed-Mode Fracture of Unidirectional Polymer Matrix Composites. Composites, B (2019) 176:107316. doi:10.1016/j.compositesb.2019.107316

CrossRef Full Text | Google Scholar

12. Liu, Y, Zhang, C, and Xiang, Y. A Critical Plane-Based Fracture Criterion for Mixed-Mode Delamination in Composite Materials. Composites, Part B (2015) 82:212–20. doi:10.1016/j.compositesb.2015.08.017

CrossRef Full Text | Google Scholar

13. Tamuzs, V, Tarasovs, S, and Vilks, U. Progressive Delamination and Fiber Bridging Modeling in Double Cantilever Beam Composite Specimens. Eng Fract Mech (2001) 68(5):513–25. doi:10.1016/S0013-7944(00)00131-4

CrossRef Full Text | Google Scholar

14. Hwu, C, Kao, CJ, and Chang, LE. Delamination Fracture Criteria for Composite Laminates. J Compos Mater (1995) 29(15):1962–87. doi:10.1177/002199839502901502

CrossRef Full Text | Google Scholar

15. Whitcomb, JD. Parametric Analytical Study of Instability-Related Delamination Growth. Compos Sci Technol (1986) 25(1):19–48. doi:10.1016/0266-3538(86)90019-9

CrossRef Full Text | Google Scholar

16. Wu, EM, and Reuter, R. Crack Extension in Fiberglass Reinforced Plastics. TAMR (1965) 275.

Google Scholar

17. Sih, GC, Paris, PC, and Irwin, GR. On Cracks in Rectilinearly Anisotropic Bodies. Int J Fract (1965) 1(3):189–203. doi:10.1007/BF00186854

CrossRef Full Text | Google Scholar

18. Allegri, G, and Scarpa, FL. On the Asymptotic Crack-Tip Stress Fields in Nonlocal Orthotropic Elasticity. Int J Sol Struct. (2014) 51(2):504–15. doi:10.1016/j.ijsolstr.2013.10.021

CrossRef Full Text | Google Scholar

19. Hussain, M, Pu, S, and Underwood, J. Strain Energy Release Rate for a Crack under Combined Mode I and Mode II. In: Fracture Analysis ASTM STP 560. Philadelphia, PA, USA: American Society for Testing and Materials (1974). p. 2–28. doi:10.1520/STP33130S

CrossRef Full Text | Google Scholar

20. Jernkvist, LO. Fracture of Wood under Mixed Mode Loading: II. Experimental Investigation of Picea Abies. Eng Fract Mech (2001) 68(5):565–76. doi:10.1016/S0013-7944(00)00128-4

CrossRef Full Text | Google Scholar

21. Yoshihara, H. Initiation and Propagation Fracture Toughness of Solid Wood under the Mixed Mode I/II Condition Examined by Mixed-Mode Bending Test. Eng Fract Mech (2013) 104:1–15. doi:10.1016/j.engfracmech.2013.03.023

CrossRef Full Text | Google Scholar

22. Sih, GC. Strain-Energy-Density Factor Applied to Mixed Mode Crack Problems. Int J Fract (1974) 10:305–21. doi:10.1007/BF00035493

CrossRef Full Text | Google Scholar

23. Jernkvist, LO. Fracture of Wood under Mixed Mode Loading: I. Derivation of Fracture Criteria. Eng Fract Mech (2001) 68(5):549–63. doi:10.1016/S0013-7944(00)00127-2

CrossRef Full Text | Google Scholar

24. Erdogan, F, and Sih, G. On the Crack Extension in Plates under Plane Loading and Transverse Shear. J Basic Eng (1963) 85(4):519–25. doi:10.1115/1.3656897

CrossRef Full Text | Google Scholar

25. Daneshjoo, Z, Shokrieh, MM, Fakoor, M, and Alderliesten, RC. A New Mixed Mode I/II Failure Criterion for Laminated Composites Considering Fracture Process Zone. Theor Appl Fract Mech (2018) 98:48–58. doi:10.1016/j.tafmec.2018.09.004

CrossRef Full Text | Google Scholar

26. Daneshjoo, Z, Shokrieh, MM, and Fakoor, M. A Micromechanical Model for Prediction of Mixed Mode I/II Delamination of Laminated Composites Considering Fiber Bridging Effects. Theor Appl Fract Mech (2018) 94:46–56. doi:10.1016/j.tafmec.2017.12.002

CrossRef Full Text | Google Scholar

27. Kaute, DAW, Shercliff, HR, and Ashby, MF. Delamination, Fibre Bridging and Toughness of Ceramic Matrix Composites. Acta Metall Mater (1993) 41(7):1959–70. doi:10.1016/0956-7151(93)90366-Z

CrossRef Full Text | Google Scholar

28. Manshadi, BD, Farmand-Ashtiani, E, Botsis, J, and Vassilopoulos, AP. An Iterative Analytical/experimental Study of Bridging in Delamination of the Double Cantilever Beam Specimen. Composites, A (2014) 61:43–50. doi:10.1016/j.compositesa.2014.02.001

CrossRef Full Text | Google Scholar

29. Sørensen, BF, Gamstedt, EK, Østergaard, RC, and Goutianos, S. Micromechanical Model of Cross-Over Fibre Bridging – Prediction of Mixed Mode Bridging Laws. Mech Mater (2008) 40(4):220–34. doi:10.1016/j.mechmat.2007.07.007

CrossRef Full Text | Google Scholar

30. Sun, Z, Hu, X, and Chen, H. Effects of Aramid-Fibre Toughening on Interfacial Fracture Toughness of Epoxy Adhesive Joint between Carbon-Fibre Face Sheet and Aluminium Substrate. Int J Adhes Adhes (2014) 48:288–94. doi:10.1016/j.ijadhadh.2013.09.023

CrossRef Full Text | Google Scholar

31. Mirsayar, MM. A Combined Stress/energy-Based Criterion for Mixed-Mode Fracture of Laminated Composites Considering Fiber Bridging Micromechanics. Int J Mech Sci (2021) 197:106319. doi:10.1016/j.ijmecsci.2021.106319

CrossRef Full Text | Google Scholar

32. Romanowicz, M, and Seweryn, A. Verification of a Non-Local Stress Criterion for Mixed Mode Fracture in Wood. Eng Fract Mech (2008) 75(10):3141–60. doi:10.1016/j.engfracmech.2007.12.006

CrossRef Full Text | Google Scholar

33. Anaraki, AG, and Fakoor, M. Mixed Mode Fracture Criterion for Wood Based on a Reinforcement Microcrack Damage Model. Mater Sci Eng A (2010) 527(27–28):7184–91. doi:10.1016/j.msea.2010.08.004

CrossRef Full Text | Google Scholar

34. Benzeggagh, ML, and Kenane, M. Measurement of Mixed-Mode Delamination Fracture Toughness of Unidirectional Glass/epoxy Composites with Mixed-Mode Bending Apparatus. Compos Sci Technol (1996) 56(4):439–49. doi:10.1016/0266-3538(96)00005-X

CrossRef Full Text | Google Scholar

35. Reeder, JR, An Evaluation of Mixed-Mode Delamination Failure Criteria, Report NASA, TM 104210. (1992). doi:10.5555/888243

CrossRef Full Text | Google Scholar

36. Ducept, F, Davies, P, and Gamby, D. An Experimental Study to Validate Tests Used to Determine Mixed Mode Failure Criteria of Glass/epoxy Composites. Composites A (1997) 28(8):719–29. doi:10.1016/S1359-835X(97)00012-2

CrossRef Full Text | Google Scholar

37. Fakoor, M, and Rafiee, R. Fracture Investigation of Wood under Mixed Mode I/II Loading Based on the Maximum Shear Stress Criterion. Strength Mater (2013) 45(3):378–85. doi:10.1007/s11223-013-9468-8

CrossRef Full Text | Google Scholar

38. van der Put, TACM. A New Fracture Mechanics Theory for Orthotropic Materials like Wood. Eng Fract Mech (2007) 74(5):771–81. doi:10.1016/j.engfracmech.2006.06.015

CrossRef Full Text | Google Scholar

39. Williams, ML. On the Stress Distribution at the Base of a Stationary Crack. J Appl Mech (1957) 24:109–14. doi:10.1115/1.4011454

CrossRef Full Text | Google Scholar

40. Reeder, JR. A Bilinear Failure Criterion for Mixed-Mode Delamination. Report NASA (1993). TM 111543. doi:10.1520/STP12636S

CrossRef Full Text | Google Scholar

41. Hintikka, P, Wallin, M, and Saarela, O. The Effect of Moisture on the Interlaminar Fracture Toughness of CFRP Laminate. In: 27th International Congress of the Aeronautical Science (2010).

Google Scholar

42. Alderliesten, R, Brunner, A, and Pascoe, J. Cyclic Fatigue Fracture of Composites: What Has Testing Revealed about the Physics of the Processes So Far. Eng Fract Mech (2018) 203:186–96. doi:10.1016/j.engfracmech.2018.06.023

CrossRef Full Text | Google Scholar

43. Cartié, D, Davies, P, Peleau, M, and Partridge, IK. The Influence of Hydrostatic Pressure on the Interlaminar Fracture Toughness of Carbon/epoxy Composites. Composites B (2006) 37(4):292–300. doi:10.1016/j.compositesb.2005.12.002

CrossRef Full Text | Google Scholar

44. de Moura, MF. Interlaminar Mode II Fracture Characterization. A volume. Woodhead Publishing Series in Composites Science and Engineering (2008). p. 310–26. doi:10.1533/9781845694821.3.310

CrossRef Full Text | Google Scholar

45. Hojo, M, Matsuda, S, Ochiai, S, Murakami, A, and Akimoto, H. The Role of Interleaf/base Lamina Interphase in Toughening Mechanism of Interleaf-Toughened CFRP. In: T Massard, and A Vautrin, editors. 12th International Conference on Composite Materials ICCM-12. Paris, France (1999). July 5–9.

Google Scholar

46. Yoshihara, H. Resistance Curve for the Mode II Fracture Toughness of Wood Obtained by the End-Notched Flexure Test under the Constant Loading Point Displacement Condition. J Wood Sci (2003) 49:210–5. doi:10.1007/s10086-002-0467-9

CrossRef Full Text | Google Scholar

47. Anh, PN, Stéphane, M, Myriam, C, and Jean-Luc, C. R-Curve on Fracture Criteria for Mixed-Mode in Crack Propagation in Quasi-Brittle Material: Application for Wood. Proced Mater. Sci. (2014) 3:973–8. doi:10.1016/j.mspro.2014.06.158

CrossRef Full Text | Google Scholar

48. Morel, S, Mourot, G, and Schmittbuhl, J. Influence of the Specimen Geometry on R-Curve Behavior and Roughening of Fracture Surfaces. Int J Fract (2003) 121:23–42. doi:10.1023/A:1026221405998

CrossRef Full Text | Google Scholar

49. Wilson, E, Mohammadi, MS, and Nairn, JA. Crack Propagation Fracture Toughness of Several Wood Species. Adv Civ Eng Mater (2013) 2(1):316–27. doi:10.1520/ACEM20120045

CrossRef Full Text | Google Scholar

Keywords: laminated composites, strain energy density, delamination, I/II mixed-mode fracture, fracture criterion

Citation: Chen X, Yuan C, Zhang W and Chen W (2025) An Improved Fracture Criterion for Mixed-Mode Delamination in Composite Materials. Aerosp. Res. Commun. 3:14365. doi: 10.3389/arc.2025.14365

Received: 18 January 2025; Accepted: 10 April 2025;
Published: 28 April 2025.

Copyright © 2025 Chen, Yuan, Zhang and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Wei Zhang, emhhbmd3ZWkwMzgxQDEyNi5jb20=; Weiqiu Chen, Y2hlbndxQHpqdS5lZHUuY24=

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.