Abstract
The ability to manipulate fluids has always been one of the focuses of scientific research and engineering application. The rapid development of machine learning technology provides a new perspective and method for active flow control. This review presents recent progress in combining reinforcement learning with high-dimensional, non-linear, and time-delay physical information. Compared with model-based closed-loop control methods, deep reinforcement learning (DRL) avoids modeling the complex flow system and effectively provides an intelligent end-to-end policy exploration paradigm. At the same time, there is no denying that obstacles still exist on the way to practical application. We have listed some challenges and corresponding advanced solutions. This review is expected to offer a deeper insight into the current state of DRL-based active flow control within fluid mechanics and inspires more non-traditional thinking for engineering.
Introduction
Despite many successful research efforts in the past decades, modifying the dynamics of flows to induce and enforce desired behavior remains an open scientific problem. In many industrial fields, researchers have placed great expectations on flow control techniques for engineering goals [1–3], such as drag reduction, noise suppression, mixing enhancement, energy harvesting. Due to the aggravation of carbon emissions and the greenhouse effect, controlling transportation drag or aerodynamic lift has become increasingly imperative.
Driven by the urgent demand from industry, active flow control (AFC) is being developed rapidly to harvest benefits for aviation or marine. As shown in Figure 1, Boeing and NASA tested a pneumatic sweeping-jet-based active flow control system on the vertical tail of the modified Boeing 757 ecoDemonstrator in April 2015. Active flow control was used to enhance the control authority of the rudder by mitigating flow separation on it at high rudder deflection, and side slip angles, which provided the required level of rudder control authority from a physically smaller vertical tail [4]. Whether using fluidic [5], micro blowing [6] or plasma actuators [7], the critical problem of active flow control is to design a reasonable control policy. The predetermined open-loop manner is the most straightforward choice. Still, the external actuation might be invalid if the evolution deviates from expectations and there are no corrective feedback mechanisms to modify the policy to compensate [8, 9]. A practical alternative is to adopt the closed-loop control manner [10–12], where the response is continuous compared with the desired result. Specifically, the control output to the process is informed by the sensors recording the flow information, then modified and adjusted to reduce the deviation, thus forcing the response to follow the reference.
FIGURE 1

A kind of flight-test AFC (Active Flow Control) system layout with photographs of hardware as installed [4].
In both ways, extensive work has been carried out by numerical simulations and experiments on exploring the nonlinear dynamics and underlying physical mechanisms of the controlled system with effective control law. For example, Xu et al. [13] investigated the separation control mechanism of a Co-flow Wall Jet, which utilized an upstream tangential injection and downstream streamwise suction simultaneously to achieve zero net-mass-flux flow control. It was found that the Co-flow wall Jet had a mechanism to grow its control capability with the increasing adverse pressure gradient. Sato et al. [14] conducted large-eddy simulations to study the separated flow control mechanism by a dielectric barrier discharge plasma actuator. From flow analysis, it was seen that an earlier and smoother transition case showed more significant improvements in the lift and drag coefficients. Moreover, the lift coefficient was improved since the actuation induced a large-scale vortex-shedding phenomenon.
While in many engineering applications, traditional large-scale physics-based models are intractable since it is required to evaluate the model to provide analysis rapidly and prediction [15–17]. The model reduction offers a mathematical foundation for accelerating physics-based computational models [18–20]. Alternatively, the model-free approach does not rely on any underlying model description of inputs to outputs. A significant advantage of a model-free manner in flow control is that it can avoid detailed identification of high-dimensional and nonlinear flow attractors, which would even shift during the regime. Moreover, with the development of machine learning techniques, it is possible to gain massive data. The control policy must grasp the embedded evolution rules and form data-driven logic. Namely, these model-free algorithms can simulate, extend and expand human intelligence to some degree.
As a critical branch of artificial intelligence, deep reinforcement learning (DRL) simplifies a stochastic dynamical system by using the framework of the Markov decision process (MDP) [22, 23]. DRL algorithms can explore and adjust control policies by interacting with the environment like a child, which gets a penalty when making mistakes. In a continuous process of trial and error, the control law in DRL learns how to get sweet lollipops (high reward) and avoid penalties. Besides, DRL utilizes the artificial neural network(ANN) as a function approximator [24]. Based on the such setting, the DRL is embedded as a state representation technology, which makes it possible to deal with high-dimensional complex problems, like Go, StarCraft, Robotics [21, 25–27]. As shown in Figure 2, Vinyals et al. [21] adopts a multi-agent reinforcement learning algorithm to train an agent named AlphaStar, in the full game of StarCraft II, through a series of online games against a human player. AlphaStar was rated at Grandmaster level for all three StarCraft races and above 99.8% of officially ranked human players. Similarly, DRL has highlighted its strong potential in fluid dynamics applications, including drag reduction, collective swimming, and flight control. Many excellent pioneers have reviewed the work related to the application of reinforcement learning in active flow control [28–32]. The present paper will further review the latest developments and demonstrate some challenges to constructing robust and effective DRL-based active flow policies.
FIGURE 2
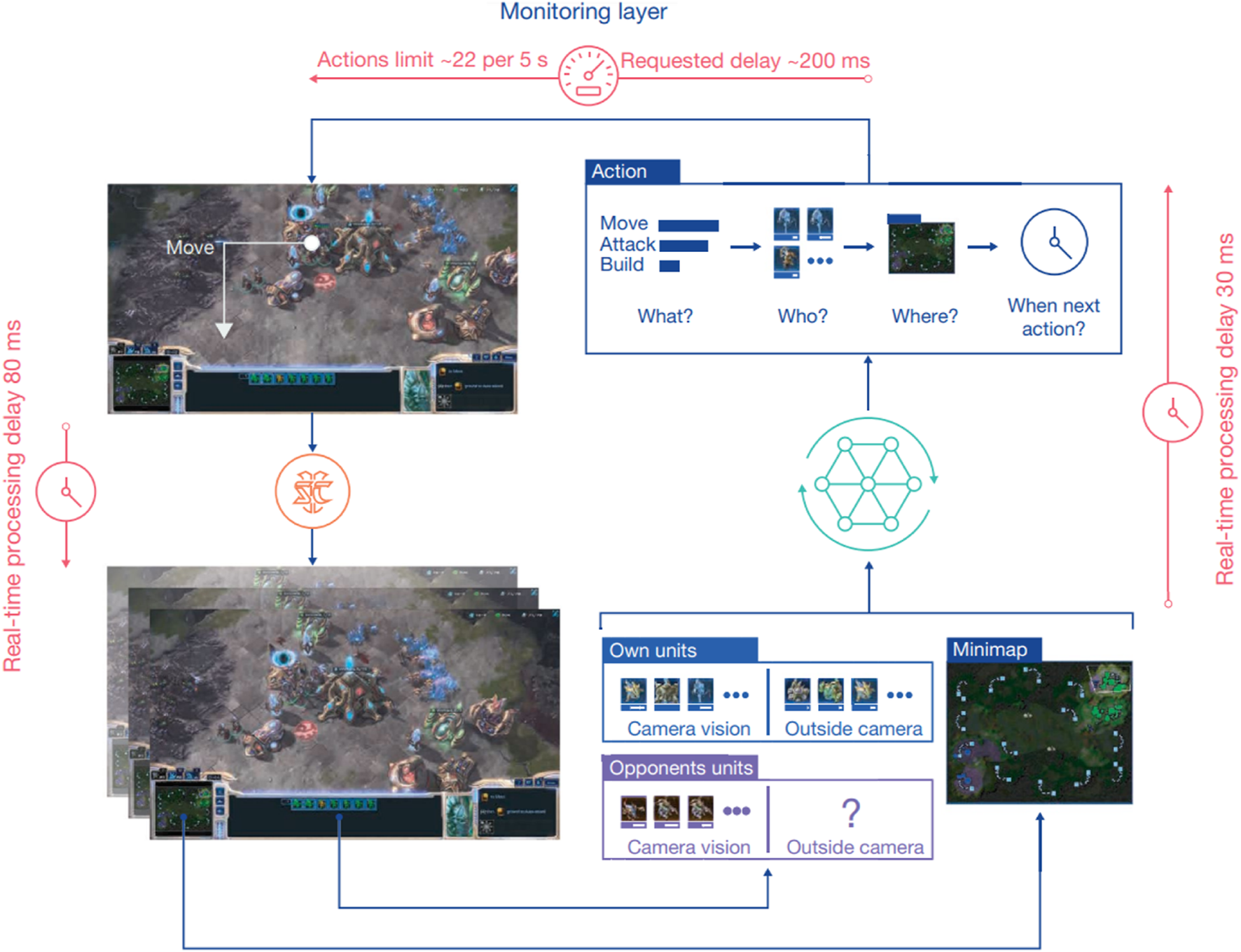
Grandmaster level in StarCraft II using multi-agent reinforcement learning. The agent observes the game through an overview map and a list of units. To act, the agent outputs what action type to issue (for example, build), who it is applied to, where its objectives are, and when the next action will be issued [21].
What needs to be mentioned is that there are many other algorithms still active on the stage that achieve great performance and have more potentials to exploit as well, such as a gradient-enriched machine learning control [33], Bayesian optimization control [34], RBF-NN adaptive control [35], ROM-based control [36]. In some work, reinforcement learning has also been compared with some algorithms, such as Bayesian optimization [37], genetic programming [38, 39], Lipschitz global optimization [39], etc. In particular, genetic programming algorithms, closely related to reinforcement learning, can achieve optimal decisions under the condition of an unknown model as well. Although the randomness of exploration brings low efficiency, evolutionary algorithms such as genetic programming are very popular in some problems like multi-objective optimization and global optimization [40, 41]. Not only in the field of flow control but algorithms combining evolutionary algorithms and reinforcement learning have also always been expected [42, 43]. For brevity, detailed comparison and discussion about the above model-free algorithms are not considered in this review, readers can refer to these papers [29, 39].
The rest of this review is organized as follows: Section Deep Reinforcement Learning presents some basic concepts and algorithms of DRL. Section Applications of DRL-based Active Flow Control offers the application of DRL on fluids problems, and Section Challenges on DRL-Based Active Flow Control shows some innovations and solutions to fluids problems to make DRL-based active flow control more effective. Finally, a summary and potential directions of DRL-based active flow control are drawn in Section Conclusion.
Deep Reinforcement Learning
This section introduces some basics concepts of typical reinforcement learning framework, and popular deep reinforcement learning algorithms, such as proximal policy optimization (PPO) [44] and soft actor-critic (SAC) [45]. First, the general terms and concepts are presented in Section Markov Decision Process. The optimization methods of reinforcement learning for policies are generally divided into Section Value-Based Methods and Section Policy-Based Methods. Either of the two methods has the ability to find the optimal control strategy. Still, their respective shortcomings must be addressed, like a relatively large gradient variance in policy method, etc. [46]. The actor-critic method discussed in Section Actor-Critic Methods, aims to combine the advantages of both ways and search for optimal policies using low-variance gradient estimates, which has been one of the most popular frameworks in reinforcement learning. Furthermore, two advanced deep reinforcement learning algorithms on the actor-critic framework are detailed in Section Advanced Deep Reinforcement Learning Algorithms.
Markov Decision Process
Reinforcement learning solves problems modeled as Markov decision processes (MDPs) [47]. The system state s, action a, reward r, time t, and reward discount factor γ are the basic concepts of MDPs. Under the intervention of action a, the system state s is transferred with a reward r. Reward r defines the goodness of action, and this transition is only related to action a and current state s, which refers to the memoryless property of a stochastic process. Mathematically, it means
Markov property helps simplify complex stochastic dynamics that are difficult to model in practice. The role of reinforcement learning is to search for an optimal policy telling which action to take in such an MDP. Specifically, the policy maps from state s and action a to the action probability distribution π, as at ∼ π(⋅|st). In the discounted reward setting, the cost function J is equal to the expected value of the discounted sum of rewards for a given policy π; this sum is also called the expected cumulative rewardwhere the trajectory τ = (s0, a0, r0, s1, a1, r1, s2, ⋯ ) is highly correlated to the policy π. And γ ∼ [0, 1) denotes the reward discount factor.
Over time, several RL algorithms have been introduced to search for an optimal policy with the greatest expected cumulative reward. They are divided into three groups [47]: actor-only, critic-only, and actor-critic methods, where the words actor and critic are synonyms for the policy and value function (policy-based and value-based), respectively. These algorithms are detailed in the following sections.
The Markov decision process can also be seen as a continuous interaction between the agent and the environment. The agent is a decision-maker that can sense the system state, maintain policies, and execute actions. Everything outside of the agent is regarded as the environment, including system state transition and action scoring [48], as shown in Figure 3. During the interaction, the agent dynamically adjusts the policy to learn behaviors with the most rewards.
FIGURE 3
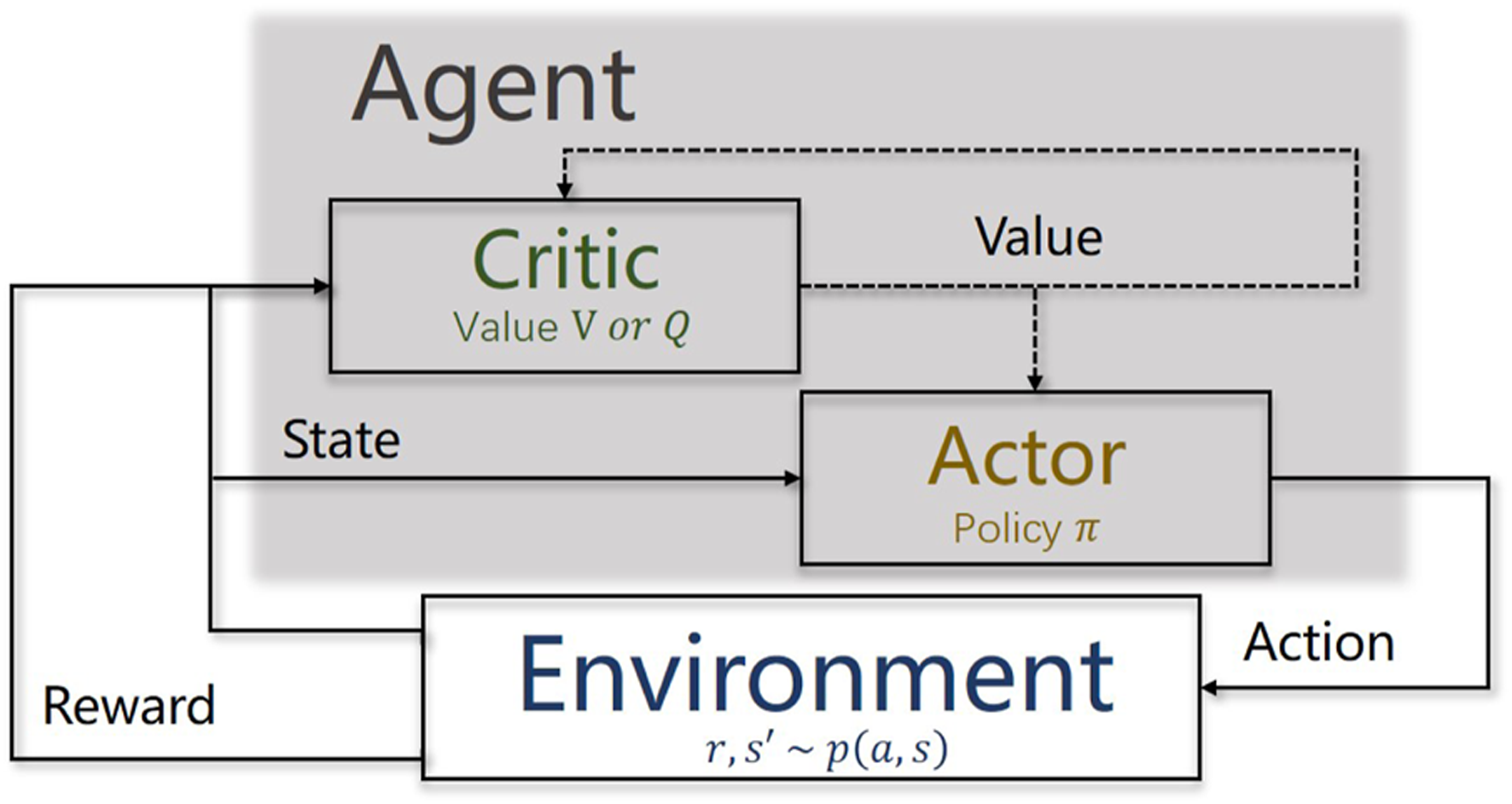
The Markov decision process of reinforcement learning. According to the reward, the agent learns to evaluate the value of each action and gain an optimal policy that maximizes the expected return.
Value-Based Methods
The value-based methods, such as Q-learning [49], SARSA [50], focus on the estimation of state value Vπ or state-action value Qπ under the specified policy π, defined as:or
As its name suggests, it represents the ”value” of a state or state-action, which is mathematically the expected value of the discounted sum of rewards with initial state s or initial state-action s − a for a given policy π. The state value Vπ(st) depends on the state st and assumes that the policy π is followed starting from this state. And the state-action value Qπ(s, a) has specified additional action at, and the future selection of actions is under policy π.
According to the Markov property of the decision-making process, the Bellman equation, a set of linear equations, is proposed to describe the relationship among values of all states:where p represents the system dynamic. The values of states rely on the values of some other states or themselves, which is related to an important concept called bootstrapping.
Since state values can be used to evaluate policies, they can also define optimal policies. If V(π1) > V(π2), π1 is said better than π2. Furthermore, if a policy is better than all the other possible policies in all states, then this policy is optimal. Optimality for state value function is governed by the Bellman optimality equation (BOE)
It is a nonlinear equation with a nice contraction property, and the contraction mapping theorem is applied to prove its convergence. The solution to the BOE always exists as the unique optimal state value, which is the greatest state value that can be achieved by any initial policy [47].
Similarly, the Bellman equation and Bellman optimality equation have expressions in terms of state-action values asand
In practice, the state-action value plays a more direct role than the state value when attempting to find optimal policies. The Bellman optimality equation is a particular form of the Bellman equation. The corresponding state value is the optimal state value, and the related implicit optimal policy can be drawn from the greatest values. For example, the optimal policy π* is calculated by using an optimization procedure over the value function:
Policy-Based Methods
The value-based methods use value functions and no explicit functions for the policy. And the policy-based methods, such as REINFORCE [51], and SRV [52], do not utilize any form of a stored value function but work with a parameterized family of policies and optimize the objective function J directly over the parameter space. Assuming that the policy is represented by a parameterized function denoted as π(a|s, θ), which is differentiable concerning parameter vector θ, the gradient of the objective function J is described as
The objective function has different metrics leading to different optimal policies. There are many metrics candidates in the policy-based methods, such as average state value, average one-step reward. If the matric is the expected cumulative reward (6), it can apply gradient descent algorithm on policy parameter θ to gradually improve the performance of the policy πθ, and the gradient is calculated as
Though in this form, the state-action value Q is called, which can be approximated by Monte Carlo estimation in REINFORCE algorithm. Based on the gradient, the parameter θ is then adjusted in the direction of this gradient:where α is the optimization rate. Every update on parameter θ seeks for an increasement on the objective function . The main advantage of policy-based methods is their strong convergence property, which is naturally inherited from gradient descent methods. Convergence is obtained if the estimated gradients are unbiased and the learning rates αk satisfy [47]
Different from the value-based methods, the policy πθ is explicit, and actions are directly sampled from the optimal parameterized policy:
Actor-Critic Methods
Value-based methods rely exclusively on value function approximation and have a low variance in the estimates of expected returns. However, when nonlinear function approximators represent value functions, the approximation bias would lead to non-convergence during numerical iterations [53, 54]. The purpose of replay buffer and target value network techniques in Deep Q-learning Network [26, 55] algorithm ameliorate the above situation well, which achieves significant progress in Atari games. Besides, value-based methods must resort to an optimization procedure in every state encountered to find the action leading to an optimal value, which can be computationally expensive for continuous state and action spaces.
Policy-based methods work with a parameterized family of policies and optimize the objective function directly over the parameter space of the policy. One of this type’s advantages is handling continuous state and action spaces with higher efficiency in terms of storage and policy searching [56]. However, a possible drawback is that the gradient estimation may have a significant variance due to the randomness of reward over time [56, 57]. Furthermore, as the policy changes, a new gradient is estimated independently of past estimates. Hence, there is no ”learning” in accumulating and consolidating older information.
Actor-critic methods aim at combining the value-based and policy-based methods [46, 58]. A parameterized function is proposed based on the value-based methods to learn state value V or state-action value Q as a critic. And the policy is not inferred from the value function. It uses a parameterized function as actor πθ, which has good convergence properties in contrast with value-based methods and brings the advantage of computing continuous actions without the need for optimization procedures on a value function. At the same time, the critic supplies the actor with low-variance value knowledge or and reduces the oscillation in the learning process.
Figure 4 shows the schematic structure of actor-critic methods. The agent consists of the critic and actor parts, which interact with the environment as presented in Section Markov Decision Process. During the collection of rewards, the critic is responsible for estimating value functions with parameterized function approximators like deep neural networks. The actor-critic methods often follow the idea of the bootstrap method to evaluate value function, whose objective function on state-action value isor on state valuebenefited from the bootstrap method, the estimation of value function or is low-variance, which is a good choice for the gradient of actor’s objective function
FIGURE 4
The actor-critic methods framework.
It is worth noting that the value-based or policy-based methods are core reinforcement learning algorithms and have played a vital role. Many techniques, like delay policy updates [59], replay buffer [26], and target value network [55], is proposed to improve the efficiency of the algorithm. The actor-critic methods are the improvement of the policy-based methods in reducing the sample variance or the expansion of the value-based method in the continuous state-action space problem. Compared to value-based or policy-based methods, the actor-critic method shows many friendly properties, a popular template for researchers developing more advanced algorithms.
Advanced Deep Reinforcement Learning Algorithms
With the deepening of research, many advanced deep reinforcement learning algorithms on the actor-critic framework have been proposed, such as PPO [44], SAC [45], TD3 [59], DDPG [60] and so on. This section presents Proximal Policy Optimization (PPO) algorithm and Soft Actor-Critic (SAC) algorithm. Considering the length of the article, a brief introduction is given. For more details and principles, interested readers are suggested to refer to the original papers [44, 45].
Proximal Policy Optimization (PPO)
Proximal policy optimization (PPO) is a robust on-policy policy gradient method for reinforcement learning proposed by OpenAI [44]. Standard policy gradient methods perform one gradient update per data sampling. Still, PPO utilizes a novel objective function that enables multiple epochs of minibatch updates by importance sampling trick, which improves sample efficiency.
Typical trust-region methods constrain policy updates to a trust region, ensuring that the entire policy update process is monotonous. PPO suggests using a KL penalty instead of a constraint to solve the unconstrained optimization problem. The algorithm is based on an actor-critic framework, and its actor objective is modified aswhere k is reuse times on single batch of data; Aθ(st, at) = Qθ(st, at) − Vθ(st, at) is the advantage function to reduce variance; β is the penalty factor of KL divergence.
PPO algorithm has the stability and reliability of trust-region methods [61]. But it is much simpler to implement, requiring only a few lines of code change to a vanilla policy gradient (VPG) implementation [47], which is applicable in general settings and has better overall performance.
Soft Actor-Critic (SAC)
Soft Actor-critic is an off-policy actor-critic deep RL algorithm based on the maximum entropy reinforcement learning framework [45]. In this framework, the actor aims to maximize the standard ultimate reward while also maximizing entropy. Maximum entropy reinforcement learning alters the RL objective [62], though the original aim can be recovered using a temperature parameter. More importantly, the maximum entropy formulation substantially improves exploration and robustness: maximum entropy policies are robust in the face of model and estimation errors, and they enhance exploration by acquiring diverse behaviors [45].
The maximum entropy objective (see, e.g., (Ziebart, 2010) generalizes the standard objective by augmenting it with an entropy term, such that the optimal policy additionally aims to maximize its entropy at each visited state:where α is the temperature parameter determining the relative importance of the entropy term against the reward. H is the entropy of policy π.
In Ref. [45], it empirically showed that it matched or exceeded the performance of state-of-the-art model-free deep RL methods, including the off-policy TD3 algorithm and the on-policy PPO algorithm without any environment-specific hyperparameter tuning. And the real-world experiments indicated that soft actor-critic was robust and sample efficient enough for robotic tasks learned directly in the real world, such as locomotion and dexterous manipulation.
Applications of DRL-Based Active Flow Control
For DRL-based active flow control, it is essential to construct a Markov Decision Process (MDP) from the flow phenomenon. If the state of flow and the reward of actions are well-selected, the reinforcement learning technique can solve the Bellman equation with high proficiency. Moreover, the artificial neural network applied to the above deep reinforcement learning algorithms has good approximation ability in high-dimensional space with less complexity than typical polynomial fitting. It has proven its advantages in many flow applications like prediction.
In the past 6 years, we have also seen many efforts to introduce deep reinforcement learning into the flow control field. From the initial tabular, e.g., Q-learning, to advanced deep learning, like Soft Actor-Critic (SAC) and Proximal Policy Optimization (PPO), DRL algorithms are equipped more smartly, and novel control phenomena have been explored. This section reviews recent flow control applications based on deep reinforcement learning, including Section Flow Stability, Section Hydrodynamic Drag, Section Aerodynamic Performance, and Section Behavior Patterns. For conciseness, a summary table is constructed as Table 1.
TABLE 1
| Category | Time | References | Algorithm | Objective |
|---|---|---|---|---|
| Flow stability | 2018 | [63] | DDPG | Control the Karman vortex shedding |
| Flow stability | 2021 | [37] | SAC,AL | Suppress the vortex-induced vibration |
| Flow stability | 2021 | [64] | PPO | Mitigate the hydrodynamic signature |
| Flow stability | 2021 | [65] | PPO | Enhance the vortex-induced vibration |
| Hydrodynamic Drag | 2017 | [66] | ML Actor-Critic | Build an implicit model and reduce drag |
| Hydrodynamic Drag | 2019 | [67] | PPO | Stabilize vortex alley and reduce drag |
| Hydrodynamic Drag | 2021 | [68] | PPO | Stabilization and drag reduction on DMD |
| Hydrodynamic Drag | 2020 | [69] | PPO | Control with small rotating cylinders |
| Hydrodynamic Drag | 2020 | [70] | PPO | Control over a range of Re numbers |
| Hydrodynamic Drag | 2022 | [71] | PPO | Control in weakly turbulent conditions |
| Hydrodynamic Drag | 2022 | [72] | PPO | Control the flow with Re = 1000 |
| Hydrodynamic Drag | 2020 | [73] | TD3 | Maximize the power gain efficiency |
| Hydrodynamic Drag | 2022 | [74] | single-step PPO | Control the wake of a 3D bluff body |
| Aerodynamic Performance | 2020 | [75] | PPO | Control on NACA0012 in pulsating inflow |
| Aerodynamic Performance | 2022 | [76] | PPO | Control lift on distributed sensors |
| Aerodynamic Performance | 2020 | [77] | DQN | Control flow separation |
| Aerodynamic Performance | 2020 | [78] | Ape-X DQN | Control flow separation |
| Aerodynamic Performance | 2022 | [79] | ApeX-DQN, ABN | Supress separation and visualize data area |
| Behavior Patterns | 2021 | [80] | DRQN | Study the behaviors of self-propelled fish |
| Behavior Patterns | 2021 | [81] | V-RACER | Learn escape under energy constraints |
| Behavior Patterns | 2022 | [82] | Q-learning | Explore collective locomotions |
| Behavior Patterns | 2018 | [83] | Q-learning | Learn glider soaring |
| Behavior Patterns | 2019 | [84] | RACER | Identify gliding and landing strategies |
Applications of DRL-based active flow control.
Flow Stability
Flow instability and transition to turbulence are widespread phenomena in engineering, and the natural environment [85–87]. The flow around a circular cylinder can be considered a prototype of the bluff body wakes, which is involved with various instability. In the cylinder wake, the transition from steady to periodic flow is marked by a Hopf bifurcation with critical Reynolds Re = 47, which is known as the first instability [88]. Three-dimensional fluctuations for higher Reynolds numbers further superimpose this vortex shedding. The onset of three-dimensionality occurs at the critical Reynolds number of Re = 175. These periodic behaviors can induce fluctuating hydrodynamic force on the bluff body, leading to vortex-induced vibrations, which can bring the challenge to structural fatigue performance or provide an opportunity for energy utilization [89, 90].
As early as 2018, Koizumi et al. [63] applied a deep deterministic policy gradient (DDPG) algorithm to control the Karman vortex shedding from a fixed cylinder. Compared with conventional model-based feedback control, the result of the DDPG also shows better control performance with reduced lift. Later on, for the vortex-induced vibrations, some scholars have also tried deep reinforcement learning to eliminate them. By constructing a spring-mounted cylinder model, Zheng et al. [37] proposed a deep reinforcement learning active flow control framework to suppress the vortex-induced vibration of a cylinder immersed in uniform flow by a pair of jets placed on the poles of the cylinder as actuators. In training, the SAC agent is fed with a lift-oriented reward, which successfully reduces the maximum vibration amplitude by 81%. Ren et al. [64] further adopted windward-suction-leeward-blowing (WSLB) actuators to control the wake of an elastically mounted cylinder. They encoded velocity information in the VIV wake into the reward function of reinforcement learning, aiming at keeping pace with the stable flow. Only a 0.29% deficit in streamwise velocity is detected, which is a 99.5% reduction from the uncontrolled value, and the learning process is shown in Figure 5. Unlike the previous two cases, instead of reducing the intensity of the vortex shedding caused by the first instability, the essence of reinforcement learning flow control in Ren’s work is to eliminate the vortex shedding caused by the first instability, which is the origin of the vortex-induced vibrations.
FIGURE 5
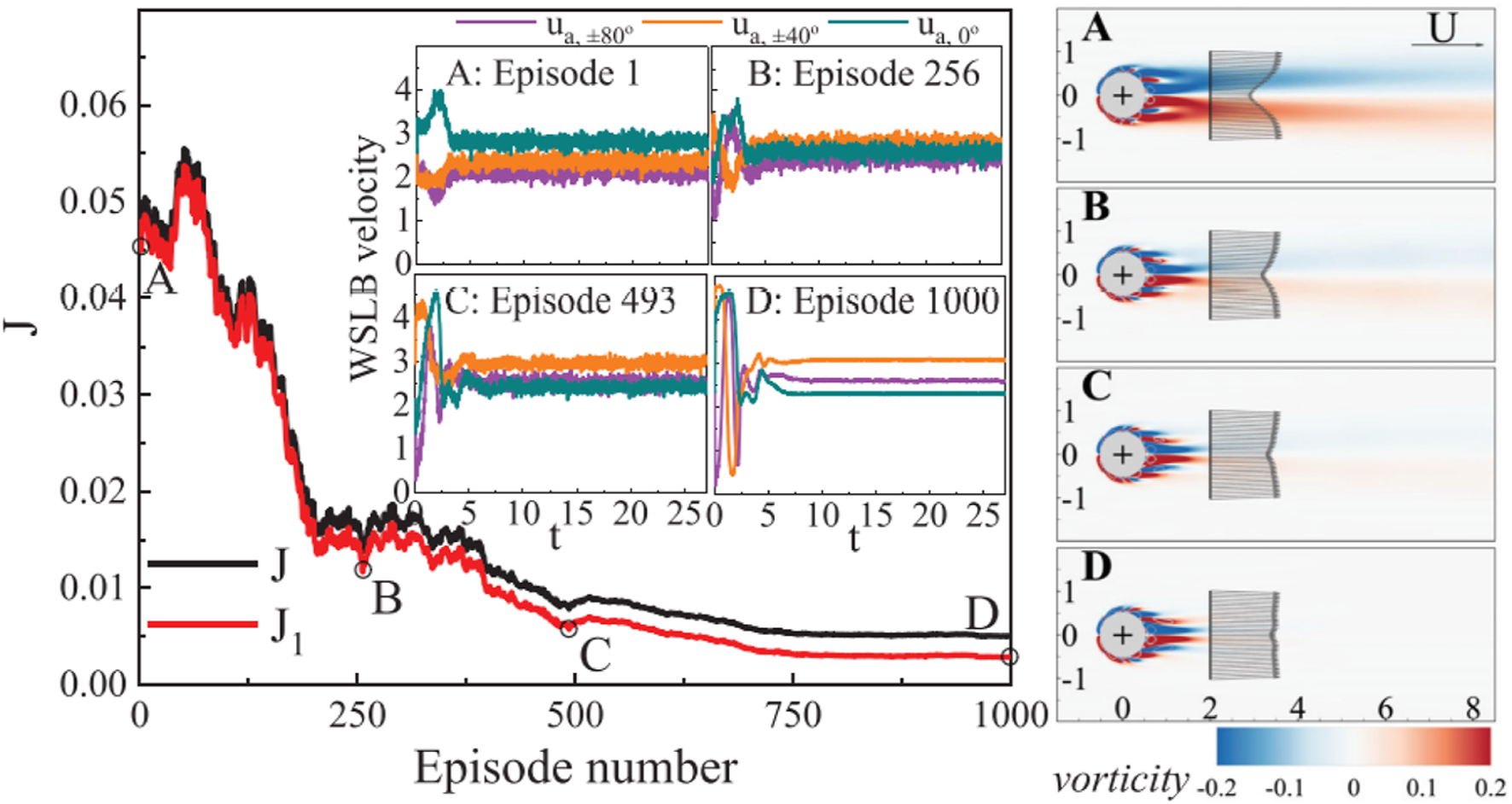
Learning process represented by the variation of objective function values against episode number. Ren and Wang adopt a group of windward-suction-leeward-blowing (WSLB) actuators to stabilize both the wake of a fixed and flexible cylinder. Left: Learning process represented by the variation of cost function values against episode number. The four insets show WSLB actuations generated by the DRL agent at different stages of learning. Right: Instantaneous wake patterns and measured velocity profiles at the four selected stages [64].
For the energy utilization of vortex-induced vibration, Mei et al. [65] proved that the performance of the active jet control strategy established by DRL for enhancing VIV is outstanding and promising. It is shown that the ANN can successfully increase the drag by 30.78% and the magnitude of fluctuation of drag and lift coefficient by 785.71% and 139.62%, respectively. Furthermore, the net energy output by VIV with jet control increased by 357.63% (case of water) compared with the uncontrolled situation.
Hydrodynamic Drag
In terms of hydrodynamic drag, it is the primary concern for modern hydrodynamic design. Namely, the potential benefits of an effective closed-loop active flow control for drag are highlighted for energy and transportation.
Like the flow stability topic, the early active flow control applications of reinforcement learning are within the deep neural network. Pivot and Mathelin [66] proposed a reinforcement learning active flow control framework whose value function and policy function are approximated with local linear models. Taking embedding and delayed effect of the action into consideration, the system’s state is constructed carefully, and 17% of cylinder drag reduction is obtained by RL-controlled self-rotating. Then the artificial neural network technique is introduced into the field of active flow control on reducing hydrodynamics drag, which replaces the original way by using elaborately-designed state representation for the flow system. Rabault [67] was the first scholar to apply an artificial neural network trained through a deep reinforcement learning agent to perform active flow control for cylinder drag reduction. At Reynolds number of Re = 100, the drag can be reduced by approximately 8% shown in Figure 6. It was seen that the circulation area is dramatically increased, and the fluctuation of vortex shedding is reduced. Their forward-looking work provided a template for DRL-based active flow control in the fluid mechanics. Qin [68] modified the reward function with dynamic mode decomposition (DMD). With the data-driven reward, the DRL model can learn the AFC policy through the more global information of the field and the learning was improved. Xu [69] used DRL to control small rotating cylinders on the back of the controlled cylinder and achieved drag reduction, which successfully illustrated the adaptability of DRL to actuators in AFC problems.
FIGURE 6
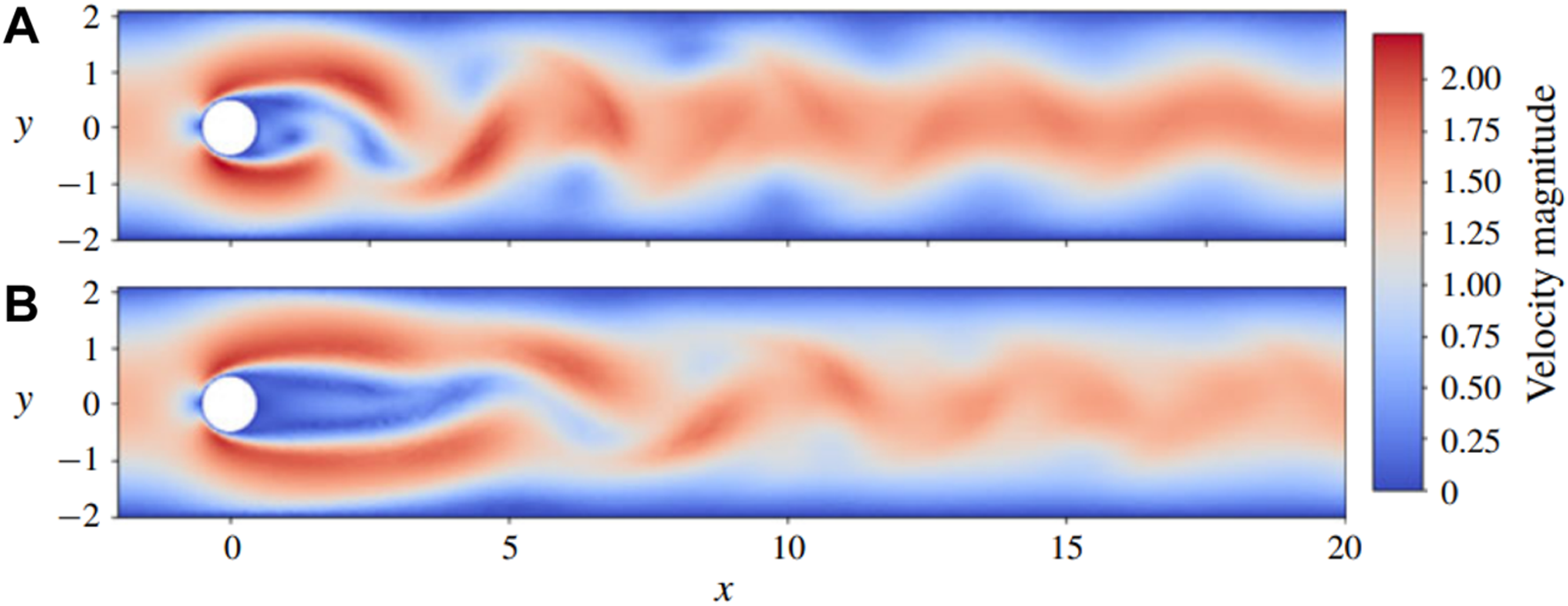
Comparison of representative snapshots of the velocity magnitude in the case without actuation (A) and with active flow control (B). The lower panel corresponds to the established pseudo-periodic modified regime, attained after the initial transient control [67].
To investigate the generalization performance of DRL, Tang [70] trained a PPO agent in a learning environment supporting four flow configurations with Reynolds numbers of 100, 200, 300, and 400, which effectively reduced the drag for any previously unrecognized value of the Reynolds number between 60 and 400. Ren [71] extended the flow condition to a weakly turbulent state with Re = 1,000 and proved that the PPO agent can still find effective control policies but requires much more episodes in the learning. For larger Reynolds numbers like 2000, Varela [72] finds significantly different forms of nature in the control strategies from those obtained at lower Re. More importantly, the cross applications of agents both from Re = 1000 and Re = 1000 were conducted in a flow with Re = 2000. Two similar results with different natures of control strategies may indicate that the Reynolds number regime (Re = 2000) belongs to a transition towards a nature-different flow which would only admit a high-frequency actuation strategy to obtain drag reduction. The deep insight is waiting for future simulations on higher Reynolds numbers.
Later on, Fan et al. [73] demonstrated the feasibility and effectiveness of reinforcement learning (RL) in bluff body flow control problems in simulations and experiments by automatically discovering active control strategies for drag reduction in turbulent flow with two small rotating cylinders. It is a crucial step to identify the limitations of the available hardware when applying reinforcement learning in a real-world experiment. After an automatic sequence of tens of towing experiments, the RL agent is shown to discover a control strategy comparable to the optimal policy found through lengthy, systematically planned control experiments. Meanwhile, the flow mechanism for the drag reduction was also explored. Through verification by three-dimensional simulations, as seen in Figure 7, due to the gap between the large and small cylinders, a jet is informed within the hole, causing the change of flow topology in the cylinder wake. Therefore, compared to the non-rotating case, the pressure on the rear cylinder surface recovered to a negative value with a smaller magnitude, leading to a significant pressure drag reduction. Moreover, with the platform of a wind tunnel, Amico et al. [74] trained an agent capable of learning control laws for pulsed jets to manipulate the wake of a bluff body at Reynolds number Re = 105. It is the first application of a single-step DRL in an experimental framework at large values of the Reynolds number to control the wake of a three-dimensional bluff body.
FIGURE 7
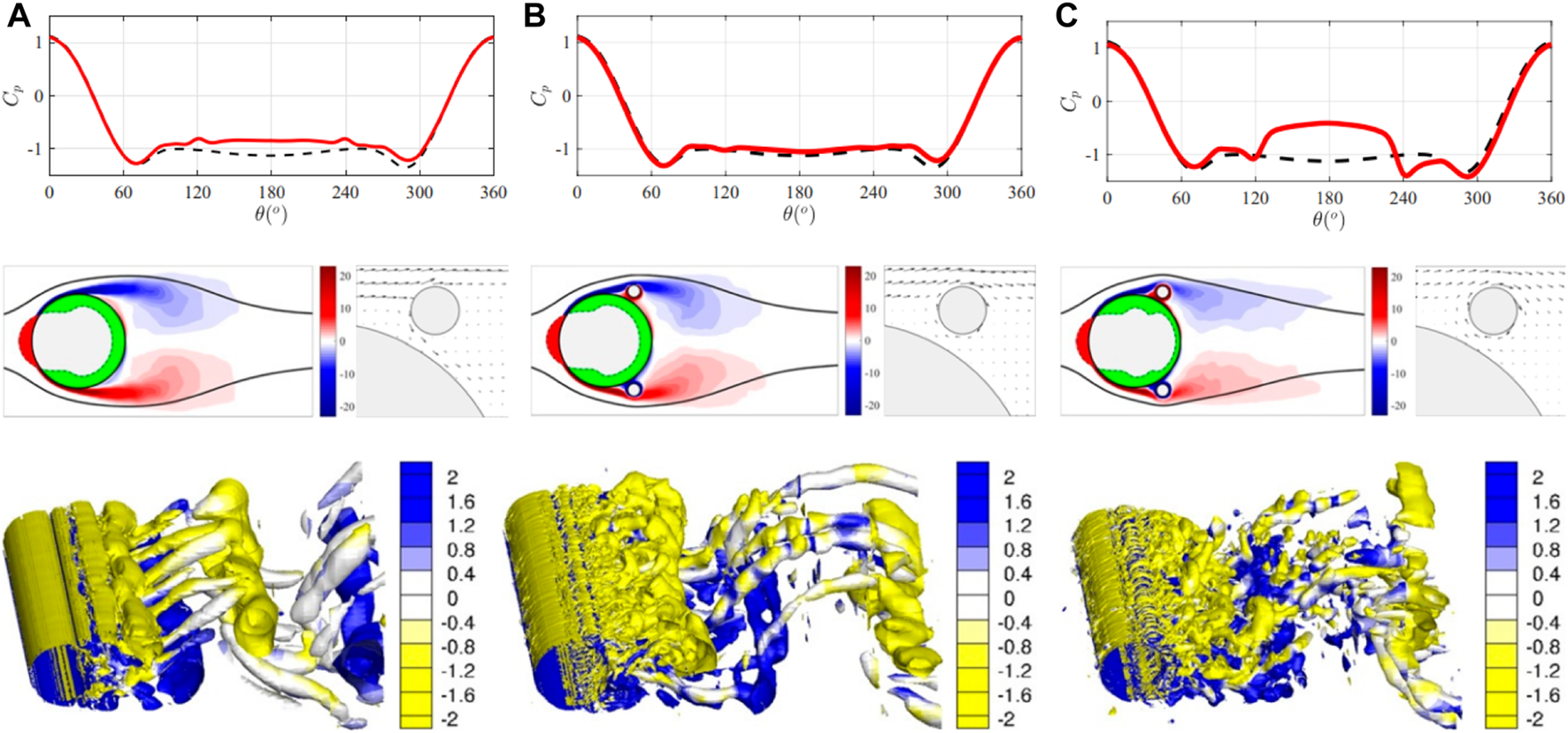
Visualization of the vortical flow at three different stages of training. (A) Before training (both small cylinders are held still). (B) After 100 episodes (both small cylinders rotate at a medium speed). (C) After 500 episodes (both small cylinders rotate at about the maximum speed). (A–C, Top) Local pressure coefficient on the cylinder surface as a function of angle (θ), with the front stagnation point as zero degrees. The coefficient is shown by the red lines, with black dashed lines representing the reference coefficient of a single cylinder. (A–C, Middle Left) the z component of vorticity averaged spanwise and in time with the green/red area indicating the magnitude of negative/positive pressure on the main cylinder. (A–C, Middle Right) Velocity field near the small upper cylinder. (A–C, Bottom) Three-dimensional vortices. Note that to plot B, we restart the simulation from the flow snapshot saved at episode 100, keep the control cylinders rotating at the same speeds as those of episode 100, and continue to simulate over two vortex-shedding periods; similar procedures are performed to obtain C [73].
Aerodynamic Performance
To make aviation greener, many efforts have been made to improve aircraft’s aerodynamic performance to design a more effective, environmentally friendly air transport system [91]. Active flow control technology can potentially deliver breakthrough improvements in the aerodynamic performance of the aircraft, like enhanced lift; reduced drag; controlled instability; and reduced noise or delayed transition. This subsection will present recent studies on DRL-based active flow control for aerodynamic performance improvement.
Several scholars have applied reinforcement algorithms to achieve effective active flow strategies through numerical simulations or wind tunnel experiments to enhance lift and reduce drag. Wang [75] used the PPO algorithm on the synthetic jet control of flows over a NACA0012 airfoil at Re = 3,000 and embedded lift information into the reward function. The DRL agent can find a valid control policy with energy conservation by 83% under a combination of two different frequencies of inlet velocity. Guerra-Langan et al. [76] trained a series of reinforcement learning (RL) agents in simulation for lift coefficient control, then validated them in wind tunnel experiments. Specifically, an ANN aerodynamic coefficients estimator is trained to estimate lift and drag coefficients using pressure and strain sensor readings together with pitch rate. Results demonstrated that hybrid RL agents that use both distributed sensing data and conventional sensors performed best across the different tests.
To suppress or delay flow separation [92], Shimomura and Sekimoto [77] proposed a practical DRL-based flow separation control framework and investigated the plasma control effectiveness on a NACA0015 airfoil in a low-speed wind tunnel at a Reynolds number of 63000. As seen in Figure 8, based on deep Q-network(DQN), the closed-loop control keeps the flow attached and preserves it for a longer time by periodically switching the actuator on and off. With distributed executors and priority experience playback, they proved that the Ape-X DQN algorithm is more stable during training than the DQN algorithm in such plasma control problem [78]. Moreover, Takada et al. [79] investigated the performance of plasma control on the NACA0012 airfoil in compressible fluid numerical simulation, which obtained the qualitative characteristics of the control policy [77].
FIGURE 8
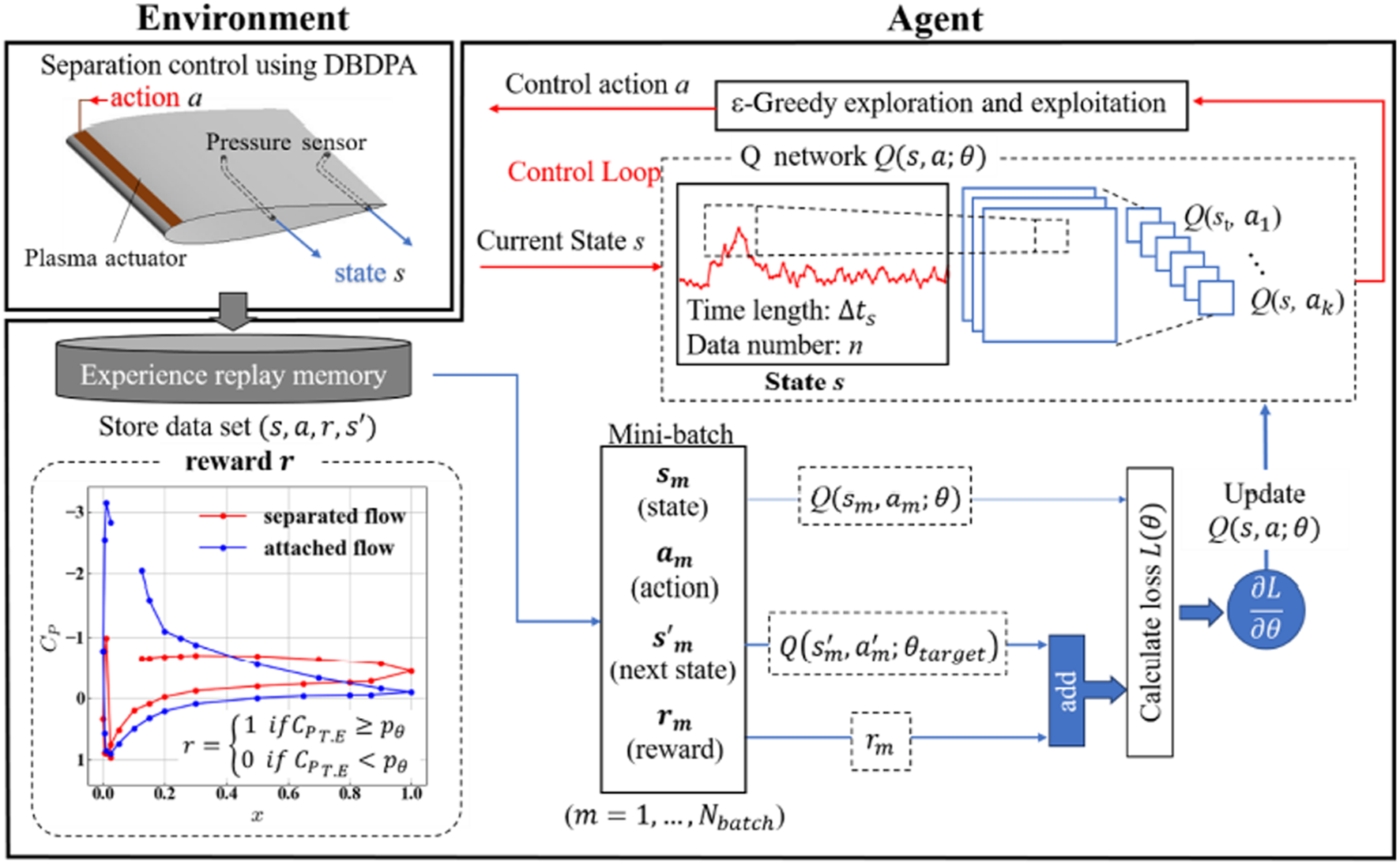
An effective DRL-based flow separation control framework [77].
Behavior Patterns
Nature’s creatures are the best teachers for researchers to discover the rule of behavior patterns, like gliders from birds that soar with thermal winds [93] or plant seeds that spread by gliding [94]. It is usually challenging to identify the internal mechanism of this adaptive pattern and generate corresponding behavior flow control strategies in another complex condition. Deep reinforcement learning has provided a new aspect to approach the goal.
In the identification and reproduction of fish adaption behaviors in complex environments, Zhu et al. [80] utilized deep recurrent Q-network (DRQN) algorithm with immersed boundary–lattice Boltzmann method to train the fish model and adapt its motion to optimally achieve a specific task, such as prey capture, rheotaxis and Kármán gaiting. Compared to existing learning models for fish, this work incorporated the fish position, velocity, and acceleration into the state space in the DRQN; it considered the amplitude and frequency action spaces and the historical effects. On the other hand, Mandralis et al. [81] deployed reinforcement learning to discover swimmer escape patterns constrained by the energy and prescribed functional form of the body motion, which can be transferred to the control of aquatic robotic devices operating under energy constraints. In addition, Yu et al. [82] numerically studied the collective locomotions of multiple undulatory self-propelled foils swimming by Q-learning algorithm. Especially swimming efficiency is the reward function, and visual information is included. It is found that the DRL algorithm can effectively discover various collective patterns with different characteristics, i.e., the staggered-following, tandem-following phalanx, and compact modes under two DRL strategies. The strategies are as follows: one is that only the following fish gets hydrodynamic advantages, and the other is that all group members take advantage of the interaction.
As for the gliding, there is also some work related to reinforcement learning, aiming at performing minimal mechanical work to control attitude. Reddy et al. [83] used Q learning to train a glider in the field to navigate atmospheric thermals autonomously, equipped with a flight controller that precisely controlled the bank angle and pitch, modulating these at intervals to gain as much lift as possible. The learned flight policy was validated through field experiments, numerical simulations, and estimates of the noise in measurements caused by atmospheric turbulence. Different from improving lift, Novati et al. [84] combined a two-dimensional model of a controlled elliptical body with DRL to achieve gliding with either minimum energy expenditure, or the fastest time of arrival, at a predetermined location. As seen in Figure 9, the model-free reinforcement learning led to more robust gliding than model-based optimal control policies with a modest additional computational cost. This study also demonstrated that the gliders with DRL can generalize their strategies to reach the objective location from previously unseen starting positions.
FIGURE 9
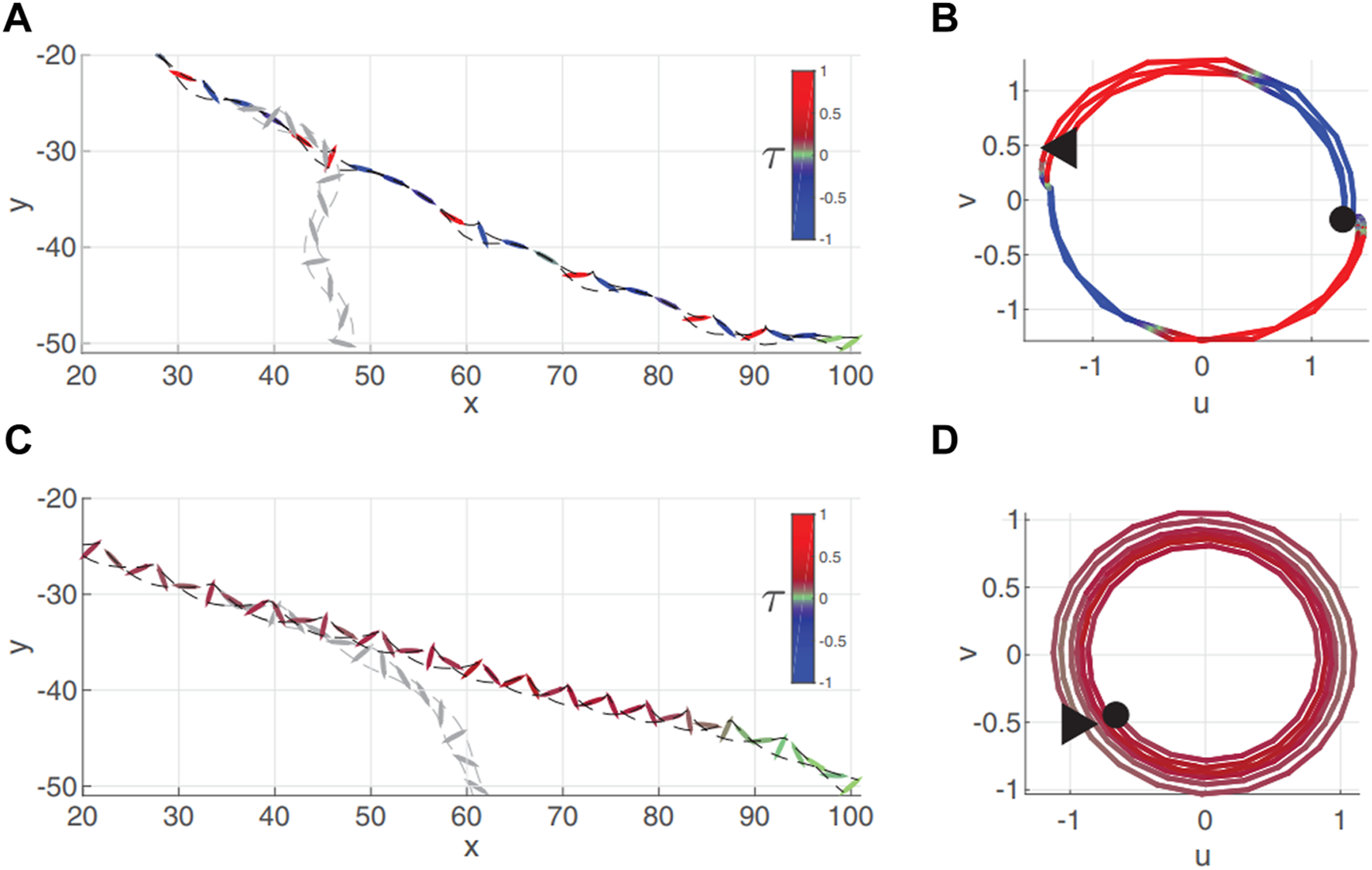
Visualization of the two prevailing locomotion patterns adopted by RL agents for the active gliding model. Trajectories on the x-y plane for (A) bounding and (C) tumbling flight. The glider’s snapshots are colored to signal the value of the control torque, and the dashed black lines track the ellipse’s vertices. The grayed-out trajectories illustrate the glider’s passive descent when abruptly switching off active control. (B, D) Corresponding trajectories on the u-v plane. The trajectories are colored based on the control torque, and a triangle and circle mark their beginning and end, respectively [84].
Challenges on DRL-Based Active Flow Control
Modern control theory provides an essential basis for developing flow control methods from open-loop control to closed-loop control. However, there may be better uses of time and resources than the detailed identification of a high-dimensional nonlinear fluid dynamical system for control. Alternatively, reinforcement learning with deep learning enables automatic feature engineering and end-to-end learning through gradient descent, so reliance on the flow mechanism is significantly reduced, shown in Section Applications of DRL-based Active Flow Control.
Though highlighted as a novel and promising direction, there are still some obstacles in the initial stage of DRL-based flow control. Some of these obstacles originate from the demand for practical reinforcement learning algorithms since direct numerical simulation, or experimental data are expensive to obtain in flow control problems. And others might be constrained by the flow control system’s characteristics, such as control delay, sensor configuration, partial observation, etc. These obstacles have come to light during the application, and researchers have specified corresponding solutions with the knowledge of the physical system. More importantly, they have revealed potential problems and provided valuable references for similar issues, which are summarized in Table 2. The following section will focus on four aspects of challenges in using DRL-based active flow control: Section Training Acceleration, Section Control Delays, Sensor Configuration, Section Partial Observables, and Section Action Dimensionality.
TABLE 2
| Category | Time | References | Algorithm | Key Words |
|---|---|---|---|---|
| Training Acceleration | 2019 | [95] | PPO | Parallelization of data collection |
| Training Acceleration | 2021 | [96] | PPO, TD3 | Expert demonstrations, behavior cloning |
| Training Acceleration | 2022 | [97] | DQN | Transfer learning, Pe numbers |
| Training Acceleration | 2022 | [98] | PPO | Transfer learning, Re numbers |
| Training Acceleration | 2022 | [99] | SAC | Expert demonstrations, off-policy buffer |
| Control Delays | 2022 | [100] | ARP–DMDP–PPO | MDP, physics-informed delay, regressive |
| Sensor Configuration | 2021 | [71] | PPO | Sensitivity analysis |
| Sensor Configuration | 2022 | [101] | PPO, DPG | Global linear stability, sensitivity analyses |
| Sensor Configuration | 2021 | [102] | S-PPO-CMA | Sparse training, stochastic gate model |
| Sensor Configuration | 2022 | [38] | PPO | Linear genetic programming control |
| Sensor Configuration | 2022 | [79] | ApeX-DQN | Attention Branch Network |
| Partial Observables | 2022 | [103] | AC | Dissipative system, low-dimensional nature |
| Action Dimensionality | 2019 | [104] | PPO | Locality and invariance, densify reward |
Challenges on DRL-based active flow control.
Training Acceleration
Essentially, deep reinforcement learning is an optimization process based on parameterized policy (usually called “agent”) through trial and error, which involves many interactions between the agent and the emulator. Therefore, compared to supervised/unsupervised learning, deep reinforcement learning is more time-consuming. Especially for the active flow control problem, the expensive data acquisition cost is required either in numerical simulation or wind tunnel experiment to represent the high dimensional flow state. On the other hand, the weakly-inductive-bias characteristic of reinforcement learning brings more possibilities and time consumption. To handle these issues, some works have been carried out on accelerating simulations or extracting prior knowledge from expert information for reinforcement learning, such as expert demonstrations, behavior cloning, or transfer learning.
From the perspective of accelerating simulation, Rabault et al. [95] demonstrated a perfect speedup by adapting the PPO algorithm for parallelization, which used several independent simulations running in parallel to collect experiences faster. As for extracting prior knowledge from expert information for reinforcement learning, Xie [96] firstly derived a simplified parametric control policy informed from direct DRL in sloshing suppression and then accelerated the DRL algorithm with a behavior cloning such simplified policy. Wang [98] transferred the DRL neural network trained with Re = 100, 200, 300 to the flow control tasks with Re = 200, 300, 1,000. As shown in Figure 10, it is due to the strong correlation between policy and the flow patterns under different conditions. Therefore a dramatic enhancement of learning efficiency can be achieved.
FIGURE 10
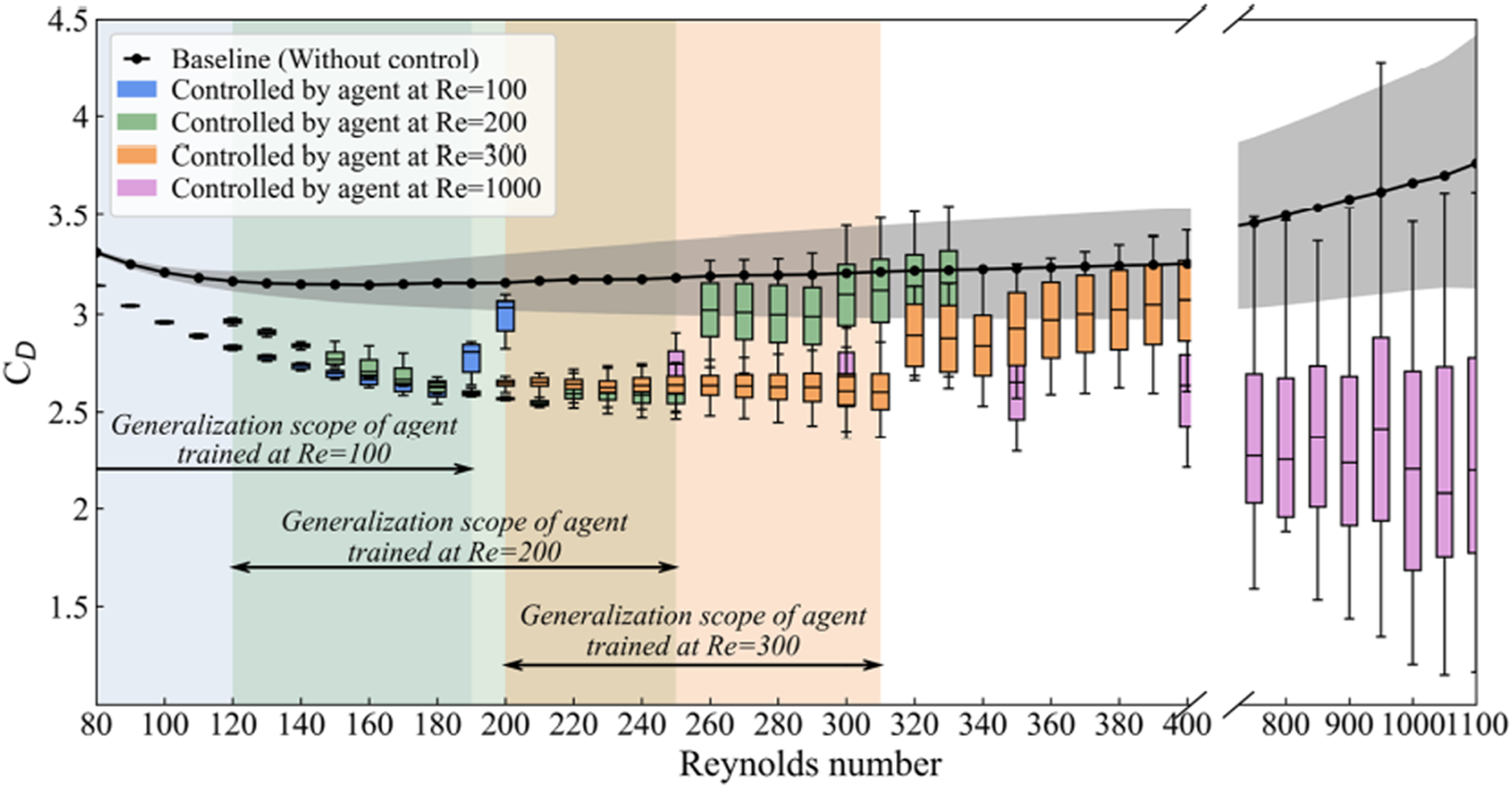
Summary of the generalization reinforcement learning test. The black line and the mean line in boxes indicate the averaged drag coefficient in the flow without and with control, respectively, and the gray shaded area and box bodies show the range of oscillation of the drag coefficient at each corresponding Reynolds number [98].
Furthermore, Konishi [97] introduced a physically reasonable transfer learning method for the trained mixer under different Péclet numbers. The balance transferability and fast learning on the Péclet number of the source domain were discussed. By filling the experience buffer with expert demonstrations, Zheng [99] proposed a novel off-policy reinforcement learning framework with a surrogate model optimization method, which enables data-efficient learning of active flow control strategies.
Control Delays
As the Reynolds number increases, temporal drag fluctuations under the DRL-controlled cylinder case tend to become increasingly more random and severe. Due to the appearance of turbulence in the state space, insufficient regression of the ANN with the time series during the decision process may result in deteriorating control robustness and temporal coherence. Due to the time elapse between actuation and response of flow, Mao [100] introduced the Markov decision process (MDP) with time delays to quantify the action delays in the DRL process by using a first-order autoregressive policy (ARP). This hybrid DRL method yielded a stable and coherent control, which resulted in a steadier and more elongated vortex formation zone behind the two-dimensional circular cylinder, hence, a much weaker vortex-shedding process and less fluctuating lift and drag forces. This method utilized the historical samples without additional training sampling than the standard DRL method. It can reduce drag and lift fluctuations by approximately 90% while achieving a similar level of drag reduction in the deterministic control at the same actuation frequency.
Sensor Configuration
In the closed-loop control framework, such as deep reinforcement learning, the sensor must be able to measure and provide a correct representation of the state of the flow system. The choice of the sensors, such as the type, number, and location, has a decisive effect on the maximum performance of the control policy. Extravagant sensor configuration is a huge and unnecessary burden in practical applications. The sensors measuring velocity, pressure, skin friction, and temperature in various resolutions, are mostly configured based on engineering experience. There is much room for improvement in adaptive algorithms, such as performing stability analysis or adopting novel optimization methods to obtain optimal and sensitive sensor locations.
In terms of stability analysis, Ren et al. [71] performed a sensitivity analysis on the learned control policies to explore the layout of the sensor network by using the Python library SALib. It is concluded that the control had different sensitivity to locations and velocity components. Li et al. [101] conducted global linear stability and sensitivity analyses based on the adjoint method. It is found that the control is most efficient when the probes are placed in the most sensitive region, and it can be successful even when a few probes are properly placed in this manner. This work is a successful example of using and embedding physical flow information in the RL-based control. The Comparison between different probe distributions is shown in Figure 11.
FIGURE 11
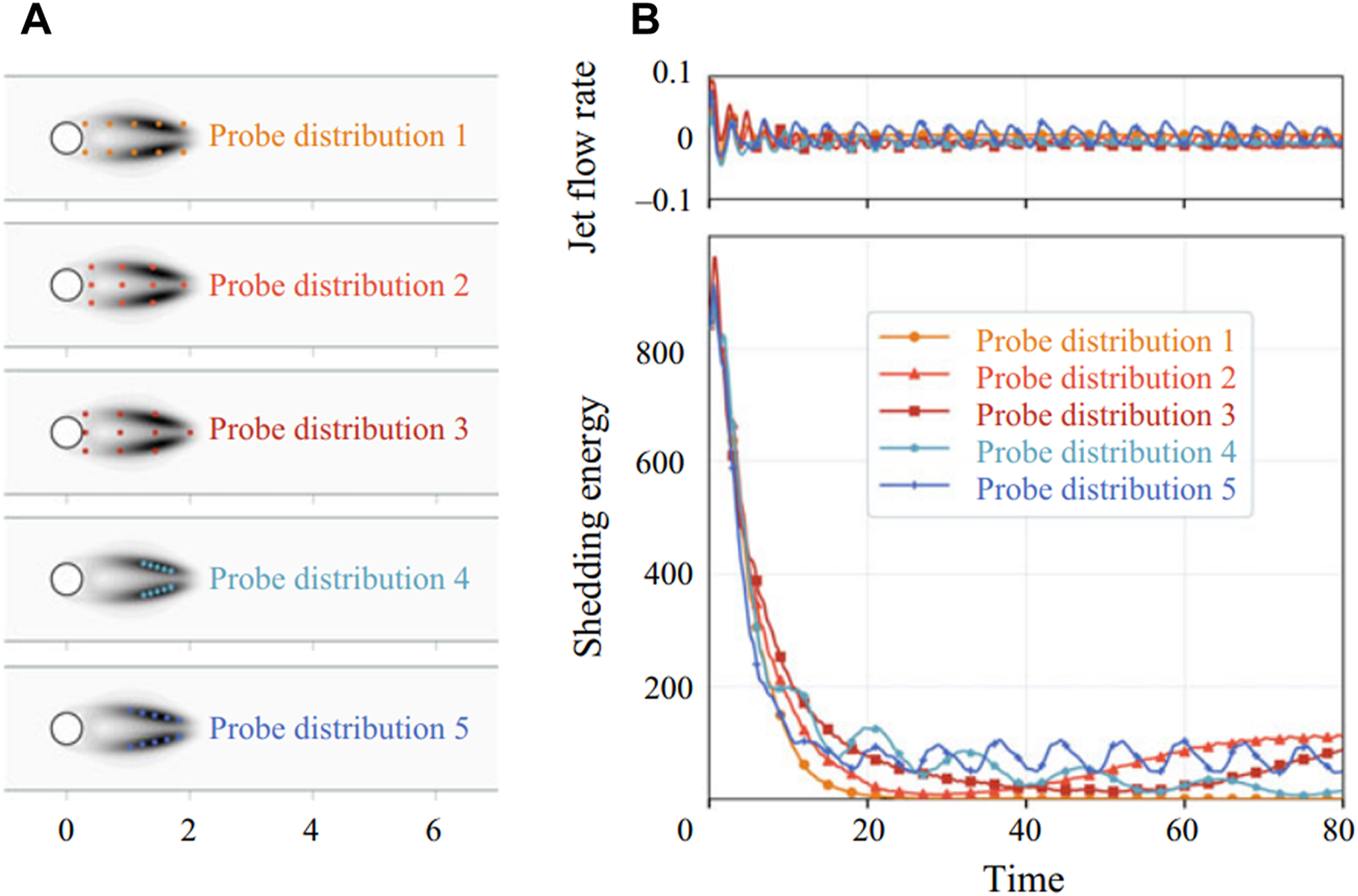
RL control of the confined cylinder wake using ten probes. Different distributions of probes lead to a significant divergence in the control performance [101]. Panel (A) shows the five types of probe distribution, and panel (B) is the corresponding control performance, including the jet flow rate and the shedding energy.
As for the optimization methods, Paris et al. [102] introduced a novel algorithm (S-PPO-CMA) to optimize the sensor layout, focusing on the efficiency and robustness of the identified control policy. Along with a systematic study on sensor number and location, the proposed sparsity-seeking algorithm achieved a successful optimization with a reduced five-sensor layout while keeping state-of-the-art performance. Castellanos et al. [38] optimized the control policy by combining deep reinforcement learning and linear genetic programming control (LGPC) algorithm, which showed the capability of LGPC in identifying a subset of probes as the most relevant locations. In addition, Takada et al. [79] have adopted a new network structure named Attention Branch Network to visualize the activation area of the DRL network, which provided references for sensor distribution. Especially, Attention Branch Network (ABN) [105] is a method to clarify the basis of the decision of neural networks, which enables the generation of an attention map to visualize the areas the neural network focuses on. It is clarified that the leading-edge pressure sensor is more important for determining the control action, and the trained neural network focused on the time variation of the pressure coefficient measured at the leading edge.
Partial Observables
Most current DRL algorithms assume that the environment evolves as a Markov decision process (MDP), and a learning agent can observe the environment state fully. However, in the real world, there are many cases where only partial observation of the state is possible. That is why existing reinforcement learning (RL) algorithms for fluid control may be inefficient under a small number of observables, even if the flow is laminar. By incorporating the dissipative system’s low-dimensional space [106] of the learning algorithm, Kubo [103] resolved this problem and presented a framework for RL that can stably optimize the policy with a partially observable condition. In the practical application of a learning process in a fluid system like a learning agent without any information about flow state except rigid-body motion, the algorithm in this study can efficiently find the optimum control method.
Action Dimensionality
Sometimes it is difficult to handle high action space dimensionality on complex tasks. Applying reinforcement learning to those tasks requires tackling the combinatorial increase of the number of possible elements with the number of space dimensions. For example, for an environment with an N-dimensional action space and n discrete sub-actions for each dimension d, using the existing discrete-action algorithms, a total of possible actions need to be considered. The number of actions that need to be explicitly represented grows exponentially with increasing action dimensionality [107].
Belus et al. [104] proposed a DRL framework to handle an arbitrary number of control actions (jets). This method relies on satisfactorily exploiting invariance and locality properties of the 1D falling liquid film system, which can be extended to other physics systems with similar properties. Inspired by the Convolutional Neural Networks (CNNs), three different methods for the DRL agent are designed as shown in Figure 12. This work set small regions in the neighborhood of each jet, where states and rewards were obtained. Methods 3 (”M3”) took into account this locality and extract N reward signals (the number of jets) to evaluate local behaviors with less dimension. Results showed both a good learning acceleration and easy control on an arbitrarily large number of jets and overcomed the curse of dimensionality on the control output size that would take place using a naive approach.
FIGURE 12
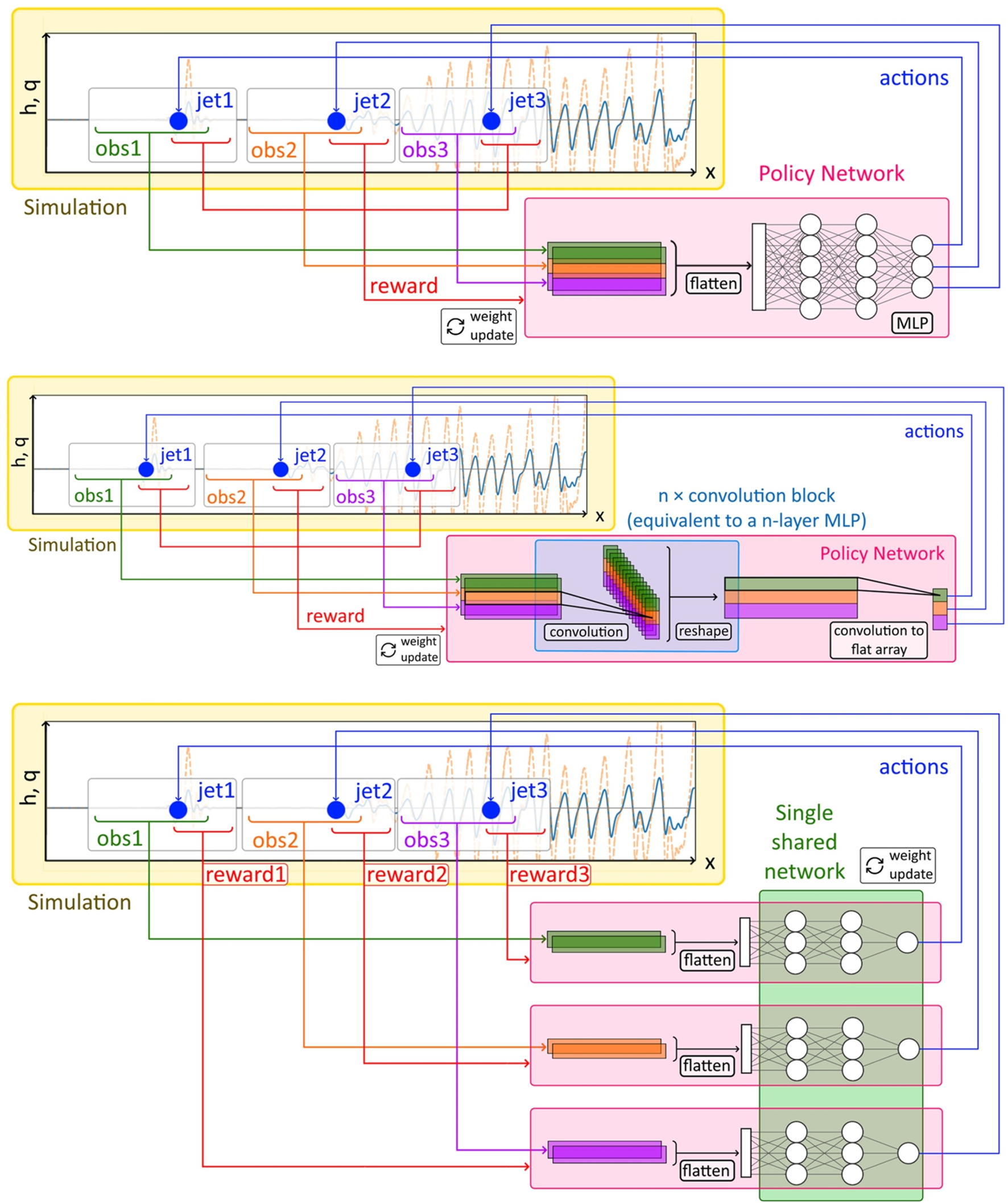
Illustration of the 3 different methods for control of a system with translational invariance and locality. From top to bottom: M1, M2, and M3. M1 is the naive implementation of the DRL framework. M2 takes advantage of translation invariance of the system to reuse the network coefficients for the control of an arbitrary number of jets. M3 exploits both the translation invariance and the locality of the system by using a dense reward signal [104].
Conclusions
Exploring flow mechanisms and controlling flow has always been one of the most important and fruitful topics for researchers. The fluid system’s high dimensionality, nonlinearity, and stochasticity limit the flow control policy exploration. It has yet to be widely applied in aviation or the marine industry. As a critical branch of artificial intelligence, reinforcement learning with deep learning enables automatic feature engineering and end-to-end learning through gradient descent so that reliance on domain knowledge is significantly reduced or even removed. Moreover, the deep and distributed representations in deep understanding can exploit the hierarchical composition of factors in data to combat the exponential challenges of the curse of dimensionality [108], which is a severe issue for the complex flow system.
Considerable research reviewed in Sections
Applications of DRL-based Active Flow Controland
Challenges on DRL-Based Active Flow Controlhas proved that deep reinforcement learning can achieve state-of-art performance in active flow control. Besides, there are other important topics which are not presented in the current review, such as optimization design [
109–
112], model discovery [
113,
114], equation solving [
115], microbiota behavior [
116–
119], plasmas magnetic control [
120], convective heat exchange [
121], chaotic system [
122]. While there are some obstacles inevitably, like the demand to accelerate the training process (Section
Training Acceleration) or the constraints related to the control system’s characteristics, such as Section
Control Delays, Section
Sensor Configuration, partial observation (Section
Partial Observables), Section
Action Dimensionality, etc. This review has introduced five topics with their solutions, and more challenges are invisible below sea level, just like icebergs. We advocate that the physical information of the flow should be embedded into the DRL-based active flow control framework. More advanced data-driven methods should be fully utilized to discover the inherent association under big data. Efficient frameworks embedded with physical knowledge under practical background can promote the wide industrial application of intelligent, active flow control technology to the greatest extent. Based on the above research and our experience, it is inferred that the study of active flow control based on deep reinforcement learning in the future can be focused on the following five aspects:
(1) Accelerate training speed and improve sample efficiency. Compared with Atari, Go, and other traditional research fields of intensive learning, the cost of data acquisition is usually higher compared to numerical simulation or wind tunnel tests. Moreover, the high-dimensional feature extraction and random system characteristics are significant challenges to the convergence of these algorithms. It is of great significance to make more rational use of data, including offline paradigm [123], model building [124], data augmentation [125], etc.
(2) Embed physical information into the reinforcement learning framework. The pure AI algorithm neglects the dynamics and believes in the data-driven concept, which is also doomed to be inefficient. It is brighter to combine the physical information into the DRL framework and develop artificial intelligence technology based on the full use of classical fluid mechanics research methods.
(3) Attain interpretability from artificial intelligence decision. Learning to control agents from high-dimensional inputs relies upon engineering problem-specific state representations, reducing the agent’s flexibility. Embedding feature extraction in deep neural networks exposes deficiencies such as a lack of explanation, limiting the application of intelligent methods. Explainable AI methods [126] are advocated to improve the interpretability of intelligent control. With the help of such practices, further exploration of more fundamental physical connotations and scientific cognition of fluid mechanics is expected.
(4) Transfer to the real world and eliminate the sim2real gap. In practical applications like aircraft flight, it is unsafe to train agents directly by trial and error. However, the reality gap between the simulation and the physical world often leads to failure, which is triggered by an inconsistency between physical parameters (i.e., Reynolds number) and, more fatally, incorrect physical modeling (i.e., observation noise, action delay). Reducing or even eliminating the sim2real gap [127] is a crucial step in applying reinforcement learning to industrial applications.
(5) Build up an open-source DRL-AFC community. The rapid development of deep reinforcement learning in the field of active flow control owes to the fact that many predecessors published the code while publishing articles. At present, we can find the work of Rabault [67, 95], Jichao Li [101], Qiulei Wang [128] and others on the Github, including containers for full reproducibility. Such sharing and openness can not only let fluid mechanics researchers understand the latest release and update of DRL tools, but also let machine learning researchers understand the development direction of algorithms applied to complex physical systems. This review calls on researchers to further share code and open source benchmarks, build a multidisciplinary open source community, further strengthen cooperation, and promote the application of reinforcement learning in the field of fluid mechanics.
To summarize, deep reinforcement learning has established the beacon for active flow control, and its talent potential in complex flow system remain to be explored. Especially in the aviation industry, it is expected that this control mode can reach unprecedented heights and realize the impossible missions in many science fiction films, for example, rudderless aircraft controlled by jets, long-endurance vehicles with weak or even no drag, etc. It is no doubt there is still a long way before DRL-based flow control realizes real-world application, but it has promised us a bright future.
Statements
Author contributions
FX: Conceptualization; Investigation; Methodology; Project administration; Resources; Writing—review and editing. CZ: Conceptualization; Methodology; Writing—original draft. TJ: Conceptualization; Funding acquisition; Investigation; Project administration; Supervision. XZ: Methodology; Conceptualization. RB: Methodology; Writing—review and editing. HZ: Investigation; Writing—review and editing. YZ: Conceptualization; Funding acquisition; Investigation; Project administration; Supervision.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1.
BowerWKibensV. An overview of active flow control applications at the boeing company. In: 2nd AIAA Flow Control Conference (2004). p. 2624. 10.2514/6.2004-2624
2.
SudinMNAbdullahMAShamsuddinSARamliFRTahirMM. Review of research on vehicles aerodynamic drag reduction methods. Int J Mech Mechatronics Eng (2014) 14(02):37–47.
3.
ZhangYYeZLiBXieLZouJZhengY. Numerical analysis of turbulence characteristics in a flat-plate flow with riblets control. Adv Aerodynamics (2022) 4(1):29–8. 10.1186/s42774-022-00115-z
4.
WhalenEAShmilovichASpoorMTranJPaulVLinJCet alFlight test of an active flow control enhanced vertical tail. AIAA J (2018) 56(9):3393–8. 10.2514/1.j056959
5.
GlezerAAmitayM. Synthetic jets. Annu Rev Fluid Mech (2002) 34(1):503–29. 10.1146/annurev.fluid.34.090501.094913
6.
XieLZhengYZhangYYeZXZouJF. Effects of localized micro-blowing on a spatially developing flat turbulent boundary layer. Flow, Turbulence and Combustion (2021) 107(1):51–79. 10.1007/s10494-020-00221-2
7.
CattafestaLNIIISheplakM. Actuators for active flow control. Annu Rev Fluid Mech (2011) 43:247–72. 10.1146/annurev-fluid-122109-160634
8.
GeorgeBHussainF. Nonlinear dynamics of forced transitional jets: Periodic and chaotic attractors. J Fluid Mech (1994) 263:93–132. 10.1017/s0022112094004040
9.
KochCRMungalMGReynoldsWCPowellJD. Helical modes in an acoustically excited round air jet. Phys Fluids A: Fluid Dyn (1989) 1(9):1443. 10.1063/1.4738832
10.
KimJThomasRB. A linear systems approach to flow control. Annu Rev Fluid Mech (2007) 39(1):383–417. 10.1146/annurev.fluid.39.050905.110153
11.
BagheriSHenningsonDSHoepffnerJSchmidPJ. Input-output analysis and control design applied to a linear model of spatially developing flows. Appl Mech Rev (2009) 62(2). 10.1115/1.3077635
12.
BruntonSLNoackBR. Closed-loop turbulence control: Progress and challenges. Appl Mech Rev (2015) 67(5). 10.1115/1.4031175
13.
XuKRenYZhaG. Separation control by co-flow wall jet. In: AIAA AVIATION 2021 FORUM (2021). p. 2946.
14.
SatoMAonoHYakenoANonomuraTFujiiKOkadaKet alMultifactorial effects of operating conditions of dielectric-barrier-discharge plasma actuator on laminar-separated-flow control. AIAA J (2015) 53(9):2544–59. 10.2514/1.j053700
15.
FarazmandMMKevlahanNKRProtasB. Controlling the dual cascade of two-dimensional turbulence. J Fluid Mech (2011) 668:202–22. 10.1017/s0022112010004635
16.
SemeraroOPralitsJORowleyCWHenningsonDS. Riccati-less approach for optimal control and estimation: An application to two-dimensional boundary layers. J Fluid Mech (2013) 731:394–417. 10.1017/jfm.2013.352
17.
CariniMPralitsJOLuchiniP. Feedback control of vortex shedding using a full-order optimal compensator. J Fluids Structures (2015) 53:15–25. 10.1016/j.jfluidstructs.2014.11.011
18.
BruntonSLKutzJN. Data-driven science and engineering: Machine learning, dynamical systems, and control. Cambridge: Cambridge University Press (2022).
19.
ZhangXJiTXieFZhengCZhengY. Data-driven nonlinear reduced-order modeling of unsteady fluid–structure interactions. Phys Fluids (2022) 34(5):053608. 10.1063/5.0090394
20.
ZhangXJiTXieFZhengHZhengY. Unsteady flow prediction from sparse measurements by compressed sensing reduced order modeling. Comput Methods Appl Mech Eng (2022) 393:114800. 10.1016/j.cma.2022.114800
21.
VinyalsOBabuschkinICzarneckiWMMathieuMDudzikAChungJet alGrandmaster level in starcraft ii using multi-agent reinforcement learning. Nature (2019) 575(7782):350–4. 10.1038/s41586-019-1724-z
22.
ArulkumaranKDeisenrothMPBrundageMBharathAA. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag (2017) 34(6):26–38. 10.1109/msp.2017.2743240
23.
François-LavetVHendersonPIslamRBellemareMGPineauJ. An introduction to deep reinforcement learning. Foundations Trends® Machine Learn (2018) 11(3-4):219–354. 10.1561/2200000071
24.
ZouJHanYSoSSLivingstoneDJ. Overview of artificial neural networks. In: Artificial neural networks. In: Methods in molecular Biology™. Totowa, NJ, USA: Humana Press (2008). p. 14–22. 10.1007/978-1-60327-101-1_2
25.
SilverDHubertTSchrittwieserJAntonoglouILaiMGuezAet alA general reinforcement learning algorithm that masters chess, shogi, and go through self-play. Science (2018) 362(6419):1140–4. 10.1126/science.aar6404
26.
MnihVKavukcuogluKSilverDGravesAAntonoglouIWierstraDet alPlaying atari with deep reinforcement learning (2013). arXiv preprint arXiv:1312.5602.
27.
KoberJBagnellJAPetersJ. Reinforcement learning in robotics: A survey. Int J Robotics Res (2013) 32(11):1238–74. 10.1177/0278364913495721
28.
RabaultJRenFZhangWTangHXuH. Deep reinforcement learning in fluid mechanics: A promising method for both active flow control and shape optimization. J Hydrodynamics (2020) 32(2):234–46. 10.1007/s42241-020-0028-y
29.
RenFHuHBTangH. Active flow control using machine learning: A brief review. J Hydrodynamics (2020) 32(2):247–53. 10.1007/s42241-020-0026-0
30.
VinuesaRLehmkuhlOLozano-DuránARabaultJ. Flow control in wings and discovery of novel approaches via deep reinforcement learning. Fluids (2022) 7(2):62. 10.3390/fluids7020062
31.
GarnierPViqueratJRabaultJLarcherAAlexanderKHachemE. A review on deep reinforcement learning for fluid mechanics. Comput Fluids (2021) 225:104973. 10.1016/j.compfluid.2021.104973
32.
ViqueratJMeligaPHachemE. A review on deep reinforcement learning for fluid mechanics: An update (2021). arXiv preprint arXiv:2107.12206.
33.
MacedaGYCLiYLusseyranFMorzyńskiMNoackBR. Stabilization of the fluidic pinball with gradient-enriched machine learning control. J Fluid Mech (2021) 917.
34.
AntoineBBMacedaGYCFanDLiYZhouYNoackBRet alBayesian optimization for active flow control. Acta Mechanica Sinica (2021) 37(12):1786–98. 10.1007/s10409-021-01149-0
35.
RenKChenYGaoCZhangW. Adaptive control of transonic buffet flows over an airfoil. Phys Fluids (2020) 32(9):096106. 10.1063/5.0020496
36.
GaoCZhangWKouJLiuYYeZ. Active control of transonic buffet flow. J Fluid Mech (2017) 824:312–51. 10.1017/jfm.2017.344
37.
ZhengCJiTXieFZhangXZhengHZhengY. From active learning to deep reinforcement learning: Intelligent active flow control in suppressing vortex-induced vibration. Phys Fluids (2021) 33(6):063607. 10.1063/5.0052524
38.
CastellanosRMacedaGYCde la FuenteINoackBRIaniroADiscettiS. Machine-learning flow control with few sensor feedback and measurement noise. Phys Fluids (2022) 34(4):047118. 10.1063/5.0087208
39.
PinoFSchenaLRabaultJMendezMA. Comparative analysis of machine learning methods for active flow control (2022). arXiv preprint arXiv:2202.11664.
40.
BanzhafWNordinPKellerREFranconeFD. Genetic programming: An introduction: On the automatic evolution of computer programs and its applications. Burlington, MA, USA: Morgan Kaufmann Publishers Inc. (1998).
41.
LangdonWBPoliR. Foundations of genetic programming. Berlin, Germany: Springer Science & Business Media (2013).
42.
MoriartyDEMikkulainenR. Efficient reinforcement learning through symbiotic evolution. Machine Learn (1996) 22(1):11–32. 10.1007/bf00114722
43.
SalimansTHoJChenXSidorSSutskeverI. Evolution strategies as a scalable alternative to reinforcement learning (2017). arXiv preprint arXiv:1703.03864.
44.
SchulmanJFilipWDhariwalPRadfordAKlimovO. Proximal policy optimization algorithms (2017). arXiv preprint arXiv:1707.06347.
45.
HaarnojaTZhouAAbbeelPLevineS. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In: International conference on machine learning. Stockholm, Sweden: PMLR (2018). p. 1861–70.
46.
KondaVTsitsiklisJ. Actor-critic algorithms. Adv Neural Inf Process Syst (1999) 12.
47.
SuttonRSBartoAG. Reinforcement learning: An introduction. Cambridge, MA, USA: MIT Press (2018).
48.
KaelblingLPLittmanMLMooreAW. Reinforcement learning: A survey. J Artif intelligence Res (1996) 4:237–85. 10.1613/jair.301
49.
WatkinsCJCHDayanP. Q-learning. Machine Learn (1992) 8(3):279–92. 10.1007/BF00992698
50.
RummeryGANiranjanM. On-line Q-learning using connectionist systems, volume 37. Cambridge, UK: University of Cambridge, Department of Engineering Cambridge, UK (1994).
51.
WilliamsRJ. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learn (1992) 8(3):229–56. 10.1007/bf00992696
52.
GullapalliV. A stochastic reinforcement learning algorithm for learning real-valued functions. Neural networks (1990) 3(6):671–92. 10.1016/0893-6080(90)90056-q
53.
TsitsiklisJVan RoyB. Analysis of temporal-diffference learning with function approximation. Adv Neural Inf Process Syst (1996) 9.
54.
MeloFSMeynSPRibeiroMI. An analysis of reinforcement learning with function approximation. In: Proceedings of the 25th international conference on Machine learning; July 5 - 9, 2008; Helsinki, Finland (2008). p. 664–71. 10.1145/1390156.1390240
55.
MnihVKavukcuogluKSilverDRusuAAVenessJBellemareMGet alHuman-level control through deep reinforcement learning. Nature (2015) 518(7540):529–33. 10.1038/nature14236
56.
SuttonRSMcAllesterDSinghSMansourY. Policy gradient methods for reinforcement learning with function approximation. Adv Neural Inf Process Syst (1999) 12.
57.
RiedmillerMPetersJSchaalS. Evaluation of policy gradient methods and variants on the cart-pole benchmark. In: 2007 IEEE International Symposium on Approximate Dynamic Programming and Reinforcement Learning. Honolulu, HI, USA: IEEE (2007). p. 254–61. 10.1109/ADPRL.2007.368196
58.
GrondmanIBusoniuLLopesGADBabuskaR. A survey of actor-critic reinforcement learning: Standard and natural policy gradients. IEEE Trans Syst Man, Cybernetics, C (Applications Reviews) (2012) 42(6):1291–307. 10.1109/tsmcc.2012.2218595
59.
ScottFHoofHMegerD. Addressing function approximation error in actor-critic methods. In: International conference on machine learning. Stockholm, Sweden: PMLR (2018). p. 1587–96.
60.
LillicrapTPHuntJJAlexanderPHeessNTomETassaYet alContinuous control with deep reinforcement learning (2015). arXiv preprint arXiv:1509.02971.
61.
SchulmanJLevineSAbbeelPJordanMMoritzP. Trust region policy optimization. In: International conference on machine learning. Stockholm, Sweden: PMLR (2015). p. 1889–97.
62.
HaarnojaTTangHAbbeelPLevineS. Reinforcement learning with deep energy-based policies. In: International conference on machine learning. Stockholm, Sweden: PMLR (2017). p. 1352–61.
63.
KoizumiHTsutsumiSShimaE. Feedback control of karman vortex shedding from a cylinder using deep reinforcement learning. In: 2018 Flow Control Conference (2018). p. 3691.
64.
RenFWangCTangH. Bluff body uses deep-reinforcement-learning trained active flow control to achieve hydrodynamic stealth. Phys Fluids (2021) 33(9):093602. 10.1063/5.0060690
65.
MeiYFZhengCAubryNLiMGWuWTLiuX. Active control for enhancing vortex induced vibration of a circular cylinder based on deep reinforcement learning. Phys Fluids (2021) 33(10):103604. 10.1063/5.0063988
66.
PivotCCordierLMathelinL. A continuous reinforcement learning strategy for closed-loop control in fluid dynamics. In: 35th AIAA Applied Aerodynamics Conference; 5-9 June 2017; Denver, Colorado (2017). p. 3566. 10.2514/6.2017-3566
67.
RabaultJKuchtaMJensenARégladeUCerardiN. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J Fluid Mech (2019) 865:281–302. 10.1017/jfm.2019.62
68.
QinSWangSRabaultJSunG. An application of data driven reward of deep reinforcement learning by dynamic mode decomposition in active flow control (2021). arXiv preprint arXiv:2106.06176.
69.
XuHZhangWDengJRabaultJ. Active flow control with rotating cylinders by an artificial neural network trained by deep reinforcement learning. J Hydrodynamics (2020) 32(2):254–8. 10.1007/s42241-020-0027-z
70.
TangHRabaultJAlexanderKWangYWangT. Robust active flow control over a range of Reynolds numbers using an artificial neural network trained through deep reinforcement learning. Phys Fluids (2020) 32(5):053605. 10.1063/5.0006492
71.
RenFRabaultJTangH. Applying deep reinforcement learning to active flow control in weakly turbulent conditions. Phys Fluids (2021) 33(3):037121. 10.1063/5.0037371
72.
VarelaPSuárezPAlcántara-ÁvilaFMiróARabaultJFontBet alDeep reinforcement learning for flow control exploits different physics for increasing Reynolds number regimes. Actuators (2022) 11:359. 10.3390/act11120359
73.
FanDLiuYWangZTriantafyllouMSKarniadakisGEM. Reinforcement learning for bluff body active flow control in experiments and simulations. Proc Natl Acad Sci (2020) 117(42):26091–8. 10.1073/pnas.2004939117
74.
AmicoECafieroGIusoG. Deep reinforcement learning for active control of a three-dimensional bluff body wake. Phys Fluids (2022) 34:105126. 10.1063/5.0108387
75.
WangYZMeiYFAubryNChenZWuPWuWT. Deep reinforcement learning based synthetic jet control on disturbed flow over airfoil. Phys Fluids (2022) 34(3):033606. 10.1063/5.0080922
76.
Guerra-LanganAAraujo EstradaSWindsorS. Reinforcement learning to control lift coefficient using distributed sensors on a wind tunnel model. In: AIAA SCITECH 2022 Forum; January 3-7, 2022; San Diego, CA & Virtual (2022). p. 0966. 10.2514/6.2022-0966
77.
ShimomuraSSekimotoSOyamaAFujiiKNishidaH. Closed-loop flow separation control using the deep q network over airfoil. AIAA J (2020) 58(10):4260–70. 10.2514/1.j059447
78.
ShimomuraSSekimotoSOyamaAFujiiKNishidaH. Experimental study on application of distributed deep reinforcement learning to closed-loop flow separation control over an airfoil. In: AIAA Scitech 2020 Forum; 6-10 January 2020; Orlando, FL (2020). p. 0579. 10.2514/6.2020-0579
79.
TakadaNIshikawaTFurukawaTNishidaH. Feedback control of flow separation over airfoil with deep reinforcement learning in numerical simulation. In: AIAA SCITECH 2022 Forum; January 3-7, 2022; San Diego, CA & Virtual (2022). p. 1365. 10.2514/6.2022-1365
80.
ZhuYTianFBYoungJLiaoJCLaiJ. A numerical study of fish adaption behaviors in complex environments with a deep reinforcement learning and immersed boundary–lattice Boltzmann method. Scientific Rep (2021) 11(1):1691–20. 10.1038/s41598-021-81124-8
81.
MandralisIWeberPGuidoNKoumoutsakosP. Learning swimming escape patterns for larval fish under energy constraints. Phys Rev Fluids (2021) 6(9):093101. 10.1103/physrevfluids.6.093101
82.
YuHLiuBWangCLiuXLuXYHuangH. Deep-reinforcement-learning-based self-organization of freely undulatory swimmers. Phys Rev E (2022) 105(4):045105. 10.1103/physreve.105.045105
83.
ReddyGWong-NgJCelaniASejnowskiTJVergassolaM. Glider soaring via reinforcement learning in the field. Nature (2018) 562(7726):236–9. 10.1038/s41586-018-0533-0
84.
GuidoNMahadevanLKoumoutsakosP. Controlled gliding and perching through deep-reinforcement-learning. Phys Rev Fluids (2019) 4(9):093902. 10.1103/physrevfluids.4.093902
85.
DrazinPG. Introduction to hydrodynamic stability, volume 32. Cambridge: Cambridge University Press (2002).
86.
SchmidPJHenningsonDSJankowskiDF. Stability and transition in shear flows. applied mathematical sciences, vol. 142. Appl Mech Rev (2002) 55(3):B57–B59. 10.1115/1.1470687
87.
ChandrasekharS. Hydrodynamic and hydromagnetic stability. Chelmsford, MA, USA: Courier Corporation (2013).
88.
JanDLe GalPFrauniéP. A numerical and theoretical study of the first hopf bifurcation in a cylinder wake. J Fluid Mech (1994) 264:59–80. 10.1017/s0022112094000583
89.
YueYXieFYanHConstantinidesYOwenOKarniadakisGEM. Suppression of vortex-induced vibrations by fairings: A numerical study. J Fluids Structures (2015) 54:679–700. 10.1016/j.jfluidstructs.2015.01.007
90.
XieFYueYConstantinidesYTriantafyllouMSKarniadakisGEM. U-shaped fairings suppress vortex-induced vibrations for cylinders in cross-flow. J Fluid Mech (2015) 782:300–32. 10.1017/jfm.2015.529
91.
AbbasADe VicenteJValeroE. Aerodynamic technologies to improve aircraft performance. Aerospace Sci Technol (2013) 28(1):100–32. 10.1016/j.ast.2012.10.008
92.
MunsonBROkiishiTHHuebschWWRothmayerAP. Fluid mechanics. Singapore: Wiley (2013).
93.
NewtonI. The migration ecology of birds. Amsterdam, Netherlands: Elsevier (2010).
94.
Shamoun-BaranesJLeshemYYom-TovYLiechtiO. Differential use of thermal convection by soaring birds over central Israel. The Condor (2003) 105(2):208–18. 10.1093/condor/105.2.208
95.
RabaultJAlexanderK. Accelerating deep reinforcement learning strategies of flow control through a multi-environment approach. Phys Fluids (2019) 31(9):094105. 10.1063/1.5116415
96.
XieYZhaoX. Sloshing suppression with active controlled baffles through deep reinforcement learning–expert demonstrations–behavior cloning process. Phys Fluids (2021) 33(1):017115. 10.1063/5.0037334
97.
KonishiMInubushiMGotoS. Fluid mixing optimization with reinforcement learning. Scientific Rep (2022) 12(1):14268–8. 10.1038/s41598-022-18037-7
98.
WangYZYueHAubryNChenZHWuWTCuiJ. Accelerating and improving deep reinforcement learning-based active flow control: Transfer training of policy network. Phys Fluids (2022) 34(7):073609. 10.1063/5.0099699
99.
ZhengCXieFJiTZhangXLuYZhouHet alData-efficient deep reinforcement learning with expert demonstration for active flow control. Phys Fluids (2022) 34:113603. 10.1063/5.0120285
100.
MaoYZhongSYinH. Active flow control using deep reinforcement learning with time delays in markov decision process and autoregressive policy. Phys Fluids (2022) 34(5):053602. 10.1063/5.0086871
101.
LiJZhangM. Reinforcement-learning-based control of confined cylinder wakes with stability analyses. J Fluid Mech (2022) 932:A44. 10.1017/jfm.2021.1045
102.
ParisRBeneddineSDandoisJ. Robust flow control and optimal sensor placement using deep reinforcement learning. J Fluid Mech (2021) 913:A25. 10.1017/jfm.2020.1170
103.
KuboAShimizuM. Efficient reinforcement learning with partial observables for fluid flow control. Phys Rev E (2022) 105(6):065101. 10.1103/physreve.105.065101
104.
VincentBRabaultJViqueratJCheZHachemERegladeU. Exploiting locality and translational invariance to design effective deep reinforcement learning control of the 1-dimensional unstable falling liquid film. AIP Adv (2019) 9(12):125014. 10.1063/1.5132378
105.
FukuiHHirakawaTYamashitaTFujiyoshiH. Attention branch network: Learning of attention mechanism for visual explanation. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. Long Beach, CA, USA: IEEE (2019). p. 10705–14. 10.1109/CVPR.2019.01096
106.
TemamR. Infinite-dimensional dynamical systems in mechanics and physics, volume 68. Berlin, Germany: Springer Science & Business Media (2012).
107.
TavakoliAPardoFKormushevP. Action branching architectures for deep reinforcement learning. Proc AAAI Conf Artif Intelligence (2018) 32. 10.1609/aaai.v32i1.11798
108.
LiY. Deep reinforcement learning: An overview (2017). arXiv preprint arXiv:1701.07274.
109.
HuiXWangHLiWBaiJQinFHeG. Multi-object aerodynamic design optimization using deep reinforcement learning. AIP Adv (2021) 11(8):085311. 10.1063/5.0058088
110.
LaiPWangRZhangWXuH. Parameter optimization of open-loop control of a circular cylinder by simplified reinforcement learning. Phys Fluids (2021) 33(10):107110. 10.1063/5.0068454
111.
HassanGViqueratJLarcherAMeligaPHachemE. Single-step deep reinforcement learning for open-loop control of laminar and turbulent flows. Phys Rev Fluids (2021) 6(5):053902. 10.1103/physrevfluids.6.053902
112.
ViqueratJRabaultJAlexanderKHassanGLarcherAHachemE. Direct shape optimization through deep reinforcement learning. J Comput Phys (2021) 428:110080. 10.1016/j.jcp.2020.110080
113.
BaeHJKoumoutsakosP. Scientific multi-agent reinforcement learning for wall-models of turbulent flows. Nat Commun (2022) 13(1):1443–9. 10.1038/s41467-022-28957-7
114.
KimJKimHKimJLeeC. Deep reinforcement learning for large-eddy simulation modeling in wall-bounded turbulence (2022). arXiv preprint arXiv:2201.09505.
115.
WeiSJinXLiH. General solutions for nonlinear differential equations: A rule-based self-learning approach using deep reinforcement learning. Comput Mech (2019) 64(5):1361–74. 10.1007/s00466-019-01715-1
116.
QiuJMousaviNZhaoLGustavssonK. Active gyrotactic stability of microswimmers using hydromechanical signals. Phys Rev Fluids (2022) 7(1):014311. 10.1103/physrevfluids.7.014311
117.
ZhuGWenFZhuL. Optimising low-Reynolds-number predation via optimal control and reinforcement learning (2022). arXiv preprint arXiv:2203.07196.
118.
BorraFBiferaleLCenciniMCelaniA. Reinforcement learning for pursuit and evasion of microswimmers at low Reynolds number. Phys Rev Fluids (2022) 7(2):023103. 10.1103/physrevfluids.7.023103
119.
TsangACHTongPWNallanSPakOS. Self-learning how to swim at low Reynolds number. Phys Rev Fluids (2020) 5(7):074101. 10.1103/physrevfluids.5.074101
120.
JonasDFeliciFJonasBNeunertMTraceyBCarpaneseFet alMagnetic control of tokamak plasmas through deep reinforcement learning. Nature (2022) 602(7897):414–9. 10.1038/s41586-021-04301-9
121.
BeintemaGCorbettaABiferaleLToschiF. Controlling Rayleigh–bénard convection via reinforcement learning. J Turbulence (2020) 21(9-10):585–605. 10.1080/14685248.2020.1797059
122.
BucciMASemeraroOAlexandreAWisniewskiGCordierLMathelinL. Control of chaotic systems by deep reinforcement learning. Proc R Soc A (2019) 475(2231):20190351. 10.1098/rspa.2019.0351
123.
LevineSKumarATuckerGFuJ. Offline reinforcement learning: Tutorial, review, and perspectives on open problems (2020). arXiv preprint arXiv:2005.01643.
124.
MoerlandTMBroekensJJonkerCM. Model-based reinforcement learning: A survey (2020). arXiv preprint arXiv:2006.16712.
125.
ConnorSKhoshgoftaarTM. A survey on image data augmentation for deep learning. J big Data (2019) 6(1):60–48. 10.1186/s40537-019-0197-0
126.
XuFUszkoreitHDuYFanWZhaoDZhuJ. Explainable ai: A brief survey on history, research areas, approaches and challenges. In: CCF international conference on natural language processing and Chinese computing; October 9–14, 2019; Dunhuang, China. Berlin, Germany: Springer (2019). p. 563–74.
127.
HöferSBekrisKHandaAGamboaJCMozifianMGolemoFet alSim2real in robotics and automation: Applications and challenges. IEEE Trans automation Sci Eng (2021) 18(2):398–400. 10.1109/tase.2021.3064065
128.
WangQYanLHuGLiCXiaoYXiongHet alDrlinfluids–an open-source python platform of coupling deep reinforcement learning and openfoam (2022). arXiv preprint arXiv:2205.12699.
Summary
Keywords
deep learning, reinforcement learning, active flow control, model-free, fluid dynamics
Citation
Xie F, Zheng C, Ji T, Zhang X, Bi R, Zhou H and Zheng Y (2023) Deep Reinforcement Learning: A New Beacon for Intelligent Active Flow Control. Aerosp. Res. Commun. 1:11130. doi: 10.3389/arc.2023.11130
Received
14 December 2022
Accepted
19 January 2023
Published
16 February 2023
Volume
1 - 2023
Updates
Copyright
© 2023 Xie, Zheng, Ji, Zhang, Bi, Zhou and Zheng.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tingwei Ji, zjjtw@zju.edu.cn
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.