Abstract
Urban Air Mobility (UAM) is considered as a powerful way to relieve urban congestion, but the noise problem is still a major obstacle to its wide application. In this paper, noise generation and propagation from dual rotors under the hovering condition are investigated without and with a phase difference of a quarter of the rotation period. The flows are simulated using large eddy simulation (LES), and the noise prediction was made through the Ffowcs Williams–Hawkings (FW-H) acoustic analogy. The results show that the rotation phase difference attenuates interactions of vortices in the wakes induced by the rotors, especially tip vortices. Furthermore, it significantly changes the spatial distribution and directivity of the noise propagation. The primary tonal noise at the first blade passing frequency is completely counteracted underneath the rotors. Noise mapping shows that a reduction of overall sound pressure levels up to 5 dB(A) is achieved in propagation directions vertical to the ground plane where the original noise levels without the rotor phase difference are large. Although a penalty to increase 3∼4 dB(A) also arises in oblique directions, the resultant noise is still low because of the original insignificant levels. The study shows that the rotor phase synchronization has important potential in the directional noise mitigation for dual-rotor systems.
Introduction
Urban Air Mobility (UAM) has attracted significant attention from both governments and industry in recent years. It is regarded as an emerging solution to alleviate urban ground traffic congestion and to expand the low-altitude economy. By 2030, UAM is expected to achieve hundreds of millions of passengers and cargo transport flights annually, generating substantial economic value [1]. Given the advancements in technologies such as electric propulsion and autonomous navigation, numerous novel electric vertical take-off and landing (eVTOL) aircraft concepts have emerged. Among them, the multirotor propulsion configuration has been widely adopted due to its strong hovering capability and adaptable maneuverability. For the purpose of validating feasibility and establishing performance metrics, NASA and other organizations have developed a series of benchmark configurations [2]. These developments underscore the significant application potential and economic implications of UAM and eVTOL technologies.
However, noise issues are widely recognized as one of the primary obstacles preventing UAM deployment [3]. As pointed out by Kim [4], UAM vehicles typically operate at low altitudes in urban settings and make frequent takeoffs and landings. Their noise is more likely to disturb residential areas, compared to large commercial aircraft flying farther. Therefore, the potential impact of UAM noise on urban communities should not be underestimated. Given operations at altitudes of approximately 300–600 m that are comparable to the height of typical urban buildings, UAM should satisfy stricter standards in noise generation and radiation [5].
According to statistics from the Vertical Flight Society (VFS), more than 1,100 eVTOL configuration designs have been developed to date, with the vast majority adopting multirotor layouts. In a multirotor system, important factors affecting noise generation and radiation are the aerodynamic interactions among rotors and between the rotors and the wing or fuselage. These interactions lead to unsteady aerodynamic force fluctuations and the emergence of additional noise sources [6, 7].
Based on these aircraft and numerous excursions, NASA has identified several key research requirements for developing air taxi aircraft, such as propulsion system efficiency, performance, rotor-rotor interactions and so on [6]. This study primarily investigates the aeroacoustic problems resulting from rotor-rotor interactions as illustrated in Figure 1 with three main eVTOL concept designs related with noise issues.
FIGURE 1

Noise challenges associated with three main eVTOL concept designs.
The wake interactions between rotors intensify unsteady loading disturbances on the rotor blades, leading to an overall increase in noise levels [7]. Intaratep et al. [8] measured a quadrotor UAV in an anechoic chamber, to compare the noise characteristics of single-, dual-, and quad-rotor configurations. They found significant spectral peak differences at the lower blade-passing frequency (BPF) harmonics for multi-rotor cases compared to the single-rotor case. In an experimental study of tandem rotors by Turhan [9], it was found that tip vortices from the upstream rotor interacted with the downstream rotor, and that the interaction varied under different rotor spacings. Two distinct noise generation mechanisms due to the interaction were identified. Aerodynamic interaction between the rotors and wing in an eVTOL can produce additional noise sources and increase the complexity of the acoustic characteristics [10]. Therefore, it is essential to conduct in-depth investigations into the aerodynamic and acoustic interference effects among multiple rotors, in order to provide guidance for noise reduction design in UAM aircraft. This will ultimately lead to quieter and more sustainable urban air mobility solutions.
In addressing the aforementioned noise issues, various blade design and passive noise reduction techniques have been widely adopted. Afari et al. [11] summarized that, for instance, bio-inspired serrations or grooves integrated into the leading or trailing edges of blades can effectively disrupt trailing-edge vortices and reduce broadband noise. Additionally, acoustic metamaterials and damping coatings have been employed to absorb or cancel noise within specific frequency ranges. These methods typically achieve noise reduction on the order of 1–3 dB, but often at the expense of degraded aerodynamic performance.
In contrast to these passive approaches with inherent aerodynamic trade-offs, phase control has emerged as a promising active noise reduction technique. Phase control refers to the adjustment of the relative angular positions of rotors in a multirotor system, so that the blade rotations exhibit specific phase differences. This difference creates interference effects in the acoustic field that can suppress noise radiation in targeted directions [12].
Both theoretical analyses and wind tunnel experiments have demonstrated the effectiveness of phase synchronization (i.e., maintaining constant phase differences) in noise reduction. Schiller et al. [12] first applied this method to an octocopter, and experimentally demonstrated that proper rotor phase control could reduce the BPF tonal noise amplitude by 4–5 dB. Guan et al. [13], through modeling and experiments, reported that a noise reduction of approximately 12 dB could be achieved from optimized phase differences. Hertzman et al. [14] further validated that, for small coaxial rotor pairs, a 90° phase difference significantly reduced the primary tonal noise by about 8 dB at a rotor speed of 3000 RPM. The study by Zhou and Fattah [15] on dual-rotor synchronization showed tonal noise reduction up to 10 dB. Recent experiments by Shao et al. [16] reached similar conclusions. On the theoretical front, Joseph [17] developed analytical models to predict the directivity and coherent cancellation of the noise generated from co-rotating and counter-rotating rotor pairs.
Although previous studies have demonstrated the potential of rotor phase control in noise reduction, there are still unknowns. Many existing experimental findings are confined to address acoustic characteristics in limited space, for example, in the vertical plane aligned with the rotation axis of a rotor [12, 15, 16], in the vertical plane in the middle of two rotors [9, 18]. Model prediction was also made in the plane of rotors [17]. Therefore, understanding and mitigating the noise mapping in a wider ground surface remain insufficient [16, 18].
The noise reduction patterns observed under such simplified conditions do not adequately reflect the actual spatial distribution of noise propagation in a real three-dimensional environment. Computational Fluid Dynamics (CFD) simulations have proven to be effective tools for studying these complex aerodynamic and acoustic interactions. For instance, Yoon et al. [19] employed high-fidelity CFD simulations to investigate flow structures and multirotor performance. Diaz [20] simulated three multirotor aircraft, which included fuselages. However, to reduce computational costs, noise prediction was mainly conducted using the unsteady Reynolds-Averaged Navier–Stokes (URANS) simulations coupled with the Ffowcs Williams–Hawkings (FW-H) acoustic analogy method [21] or theoretical modes with the FW-H method [22]. They studied the effects of parameters such as the number of rotors, rotor tip spacing, and rotor phase angles.
This study aims to conduct a numerical investigation on phase-synchronized noise reduction for a representative dual-rotor configuration under phase offsets such as 0° and 90°. To understand the directivity and intensity of far-field noise in three dimensions, the noise mapping and noise counteraction will be addressed. Large eddy simulation (LES) will be used for the flow simulation, and it will be coupled with the FW-H acoustic analogy for the noise prediction.
Simulation Methodology
Geometrical Model
The geometry was constructed based on the two-bladed rotor of DJI-9450, of which the diameter is 0.24 m. The thickness and twist angle distribution of the blade along the radial direction is illustrated in Figure 2. Both parameters reach the maximum values near of the blade spanwise length. And the chord and thickness at the blade tip are much smaller than those at the blade root.
FIGURE 2
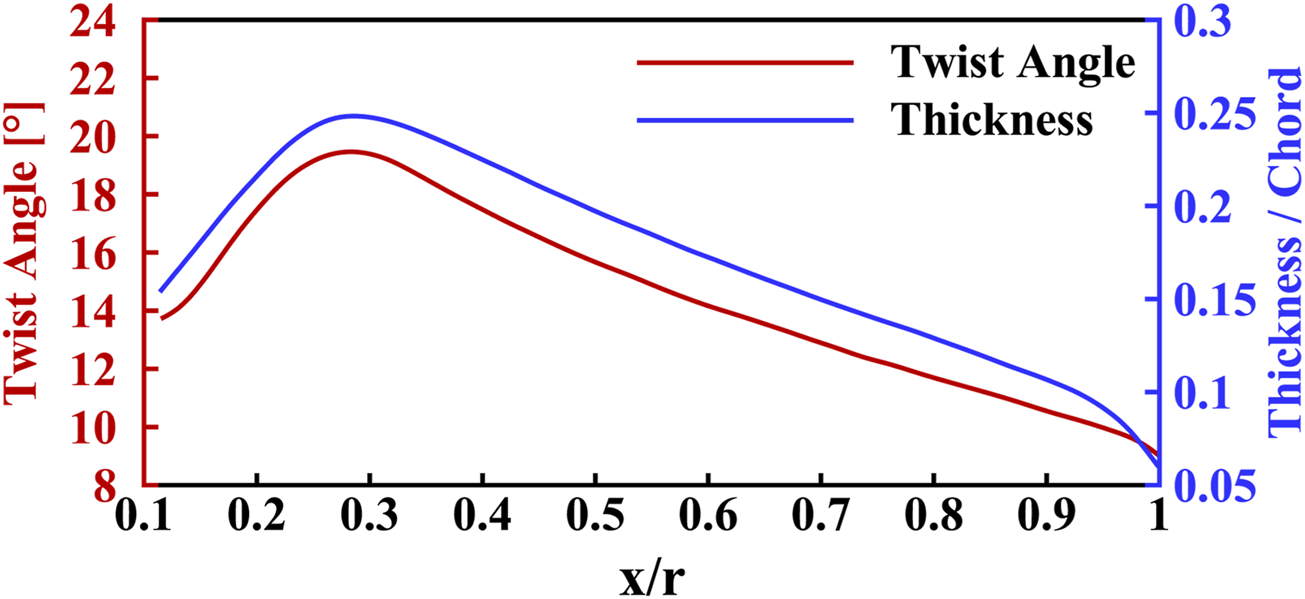
Distribution of the thickness and twist angle parameters of the blade in the radial direction.
The dual-rotor systems with different initial phases, ° and °, are shown in Figure 3. Here in the case of 0°, the two rotors are aligned with the same phase angle, whereas 90° leads to the phase angles of the rotors being normal to each other. The distance between the rotors is 0.1D, where D is the rotor diameter. The hover condition, without the consideration of the forward flight speed, was simulated. A representative rotational speed of 5400 RPM was considered, corresponding to the BPF of 180 Hz.
FIGURE 3
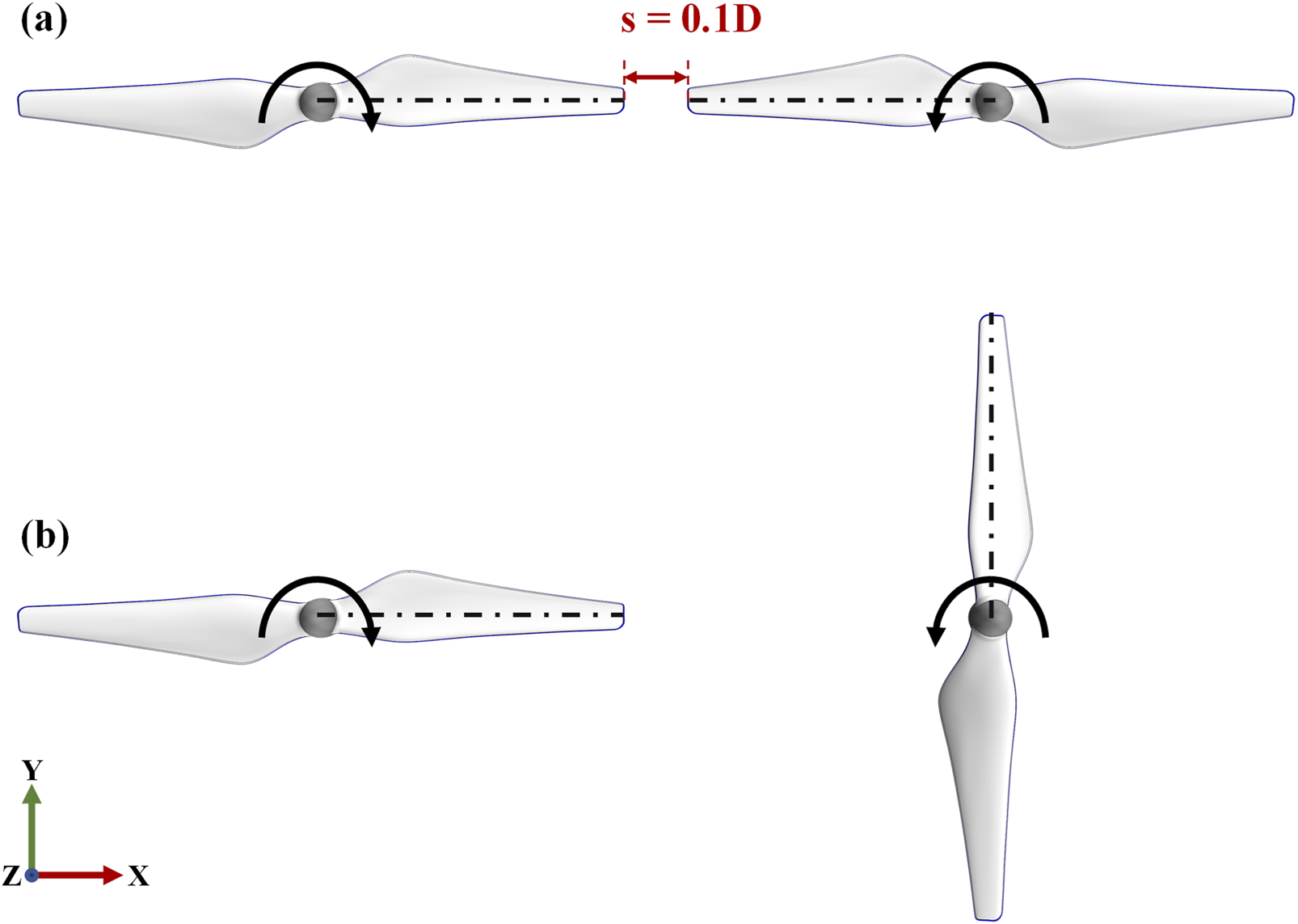
Schematic of the dual-rotor systems with the phase angles: (a)° and (b) °.
Numerical Method
The compressible flow modelled as an ideal gas was simulated using a LES approach based on Star-CCM+ [23]. The Wall-Adapting Local Eddy-viscosity (WALE) model was used for subgrid-scale turbulence modeling. The all-y+ treatment approach was applied near the walls, which enables the mesh to accommodate both fine and coarse resolution for capturing the characteristics of turbulent boundary layers.
The governing equations were discretized using a finite element method with the segregated algorithm. The convection terms were discretized with a hybrid scheme of second-order central differencing, for low numerical dissipation in smooth regions, and upwind biasing for numerical stability in regions with sharp gradients. The terms of diffusion, pressure gradient and viscous stresses were discretized using a second-order central differencing scheme. The time marching scheme adopted an implicit second-order backward differencing. The time step was chosen to satisfy the Courant–Friedrichs–Lewy (CFL) number less than one.
A non-reflecting boundary condition was applied to the far-field boundaries of the computational domain, to mitigate spurious acoustic reflections. The far-field noise was predicted using the FW-H acoustic analogy of Formulation 1A and the acoustic pressure signals on the rotor surface are propagated to far-field receivers. The solid surfaces of the rotors were selected as the integration surfaces for the FW-H acoustic analogy. This approach is justified since the relative Mach number at the blade tip under hover conditions is less than 0.2 in the current simulation cases. At such relatively low Mach numbers, the contribution of quadrupole sources is negligible, making the solid-surface formulation both computationally efficient and sufficiently accurate. For cases involving higher Mach numbers, however, the quadrupole sources cannot be neglected, and the use of a permeable integration surface would be necessary for accurate far-field noise prediction.
Computational Domain Setup and Meshing
The computational domain was defined as a cylindrical volume enclosing the dual-rotor system, as shown in Figure 4. The origin of the global coordinate system is located in the middle of the gap between the rotors. The length scales labeled in the figure are normalized by the rotor diameter D. The diameter of the computational domain is 8, and it streamwise length is 10 with 2 upstream of the rotor plane and 8 downstream. A sliding mesh approach is employed to capture the rotor motion, wherein two rotating subdomains are defined to contain the rotors. Boundary conditions are specified as follows: the top boundary is prescribed as a pressure inlet, while the side and bottom boundaries are treated as pressure outlets. The rotor surfaces are set as no-slip walls.
FIGURE 4
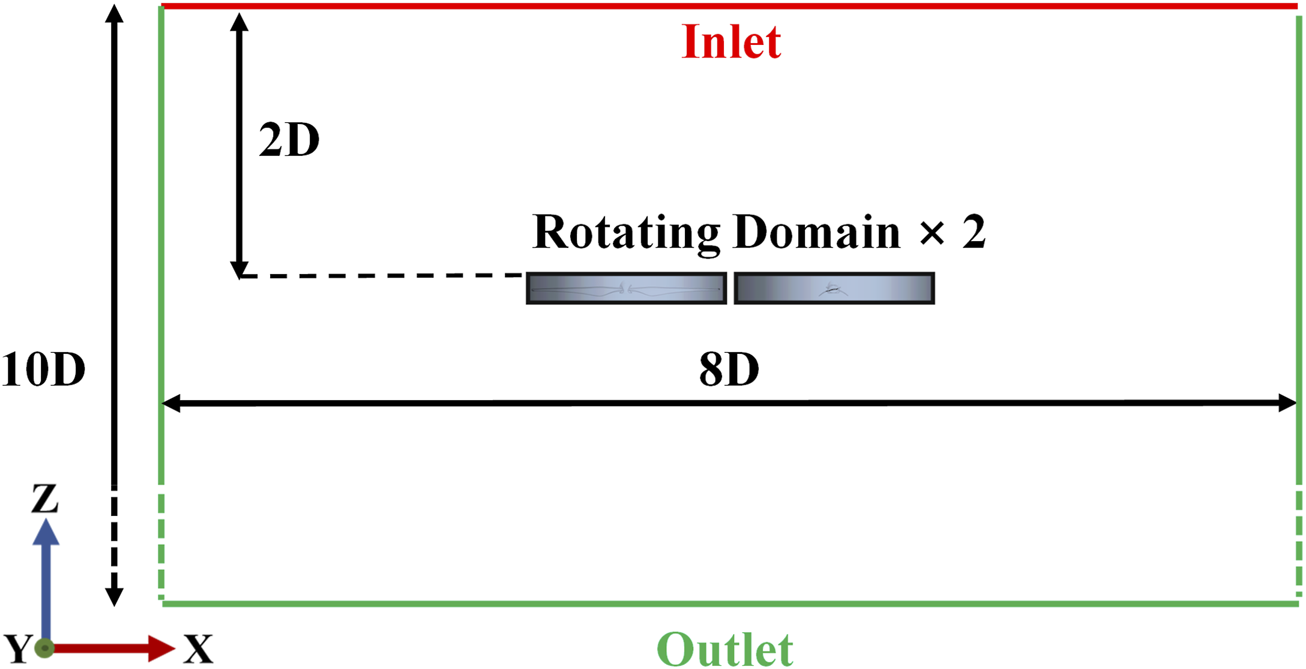
Schematic of the computational domain.
To ensure the numerical accuracy in resolving near-field flow structures and computing the far-field noise using the FW-H acoustic analogy, the computational meshes were refined in specific zones where flow vortices are intensive. Volume and surface cells in cut-planes and the walls are illustrated shown in Figure 5. A volume refinement zone with a base cell size of 5e-4 m was established within 4 mm offset from the rotor walls. Outside of this zone, a second-level refinement was set with a base cell size of 1e-3m. Near the leading edges, trailing edges and tips of the blades, the base grid size was set between 1.25e-4 mm and 2.5e-4 m. The first layer height of near-wall cells was 2e-6 m, and there are 25 prism layers with a growth ratio 1.2, forming a total thickness of 1e-3 m to resolve the boundary layers. The mesh contained 5.36 million cells in each rotating subdomain and 12.8 million cells in the outer stationary subdomain.
FIGURE 5
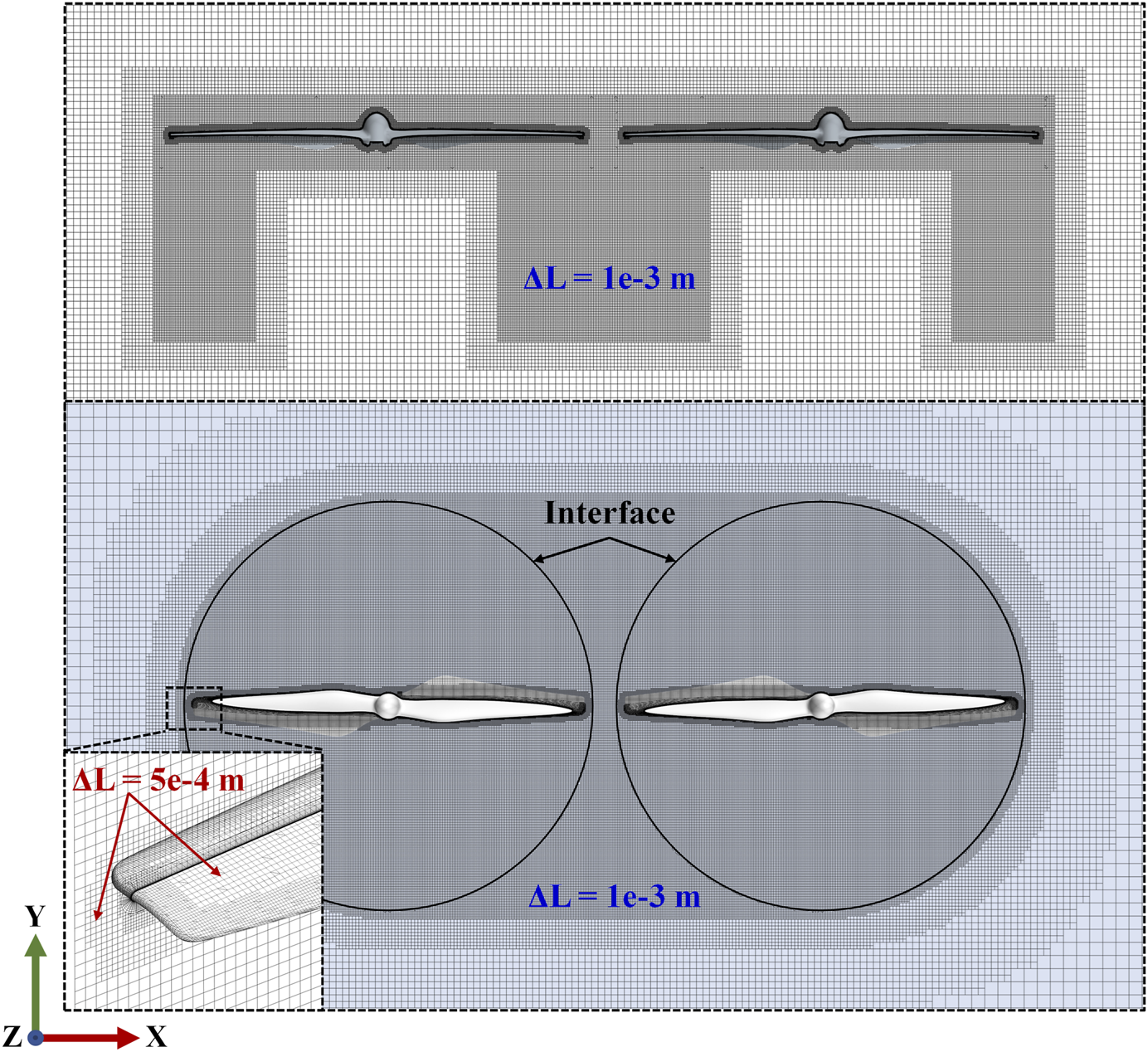
Surface and volume cell sizes defined in the computational mesh.
Results
Validation of Numerical Methodology
An isolated DJI-9450 rotor was studied as the reference for validation. The pressure coefficient distribution along the blade chord at the spanwise section of 0.5R is shown in Figure 6. The present results were compared to the simulation data from Christopher et al. [24] using PowerFLOW, which was programmed based on the lattice Boltzmann Method integrated with the Very Large Eddy Simulation (LBM-VLES), and also compared to the results using XFOIL (based on the potential flow theory) and FUN3D. It is observed that the present results align well with the high-fidelity LBM-VLES results, particularly in capturing critical flow characteristics such as the suction-side pressure peak and the leading-edge pressure gradient. This confirms the accuracy of the present numerical method.
FIGURE 6
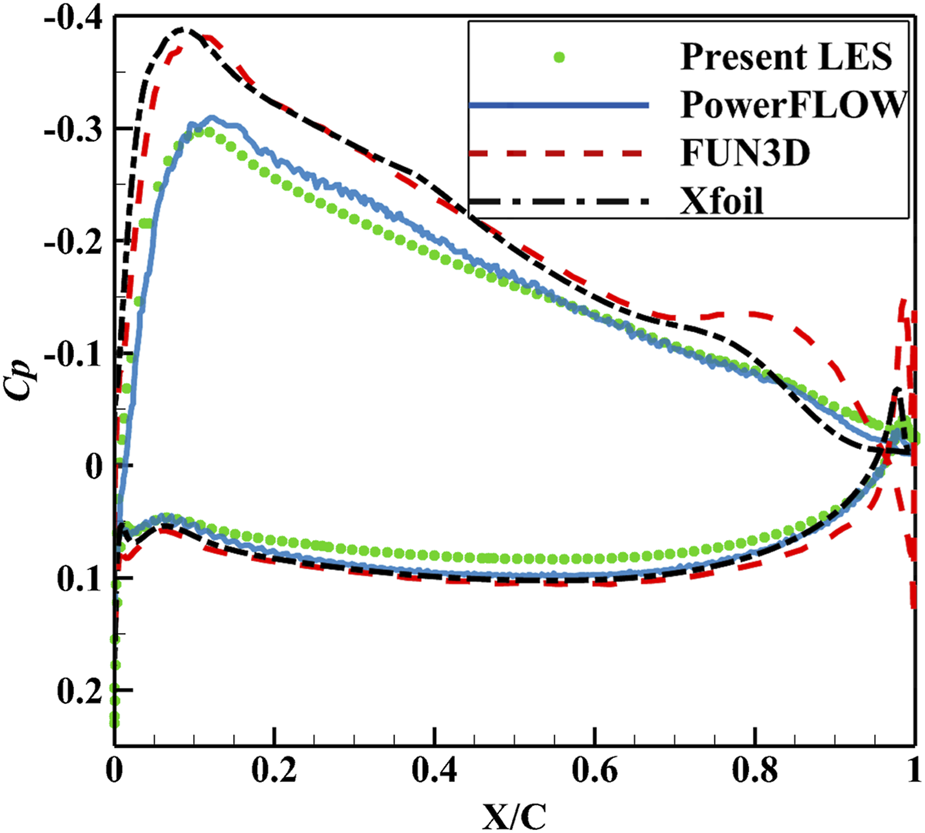
Surface pressure coefficient along the chord at the radial position of 0.5 rotor radius.
To further demonstrate the rationality of the computational setup, Figure 7 illustrates the y+ distribution on the dual-rotor surfaces. Given that the y+ values are generally small and remain below 5, the use of a low Reynolds number wall treatment would also be reasonable. However, due to the geometric complexity of the rotors, localized regions with relatively coarse mesh resolution may occur especially near intricate corners. These areas are often difficult to identify and correct thoroughly. Therefore, we adopted an all-y+ wall treatment to avoid potential inaccuracies that might be overlooked. This method automatically switches to a low Reynolds number mode in regions with sufficiently refined near-wall grids, achieving consistent behavior with a dedicated low-y+ treatment while ensuring robustness across the entire computational domain.
FIGURE 7
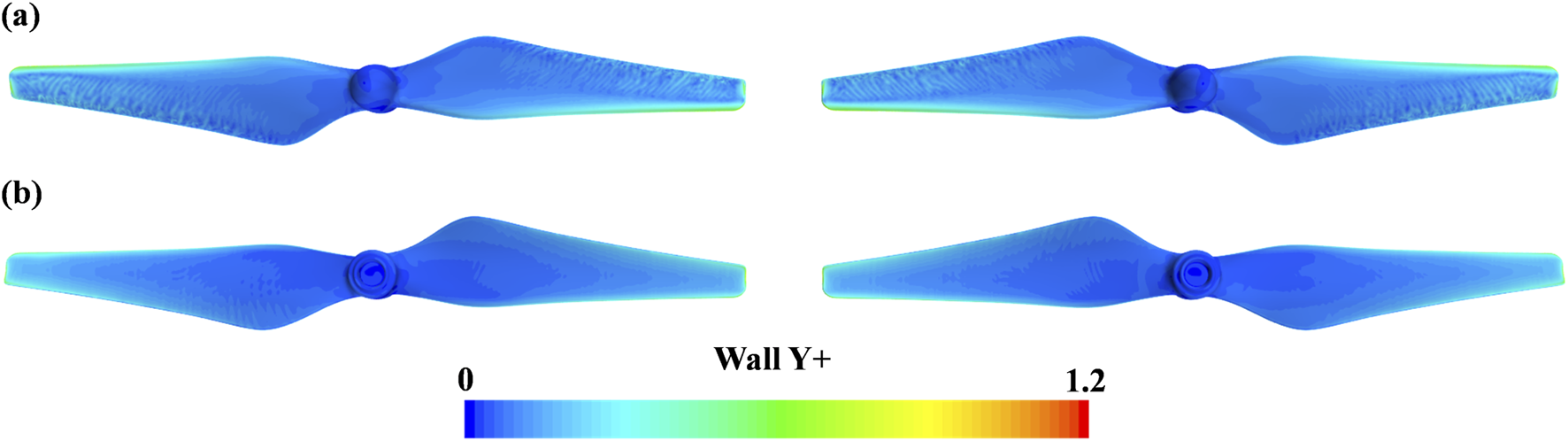
Wall Y + distribution on blade surface. (a) Top surface, (b) Bottom surface.
The current noise prediction was compared to a theoretical model and experimental measurements. The theoretical model for tonal noise was originally developed by Hanson and Parzych [25]. This model builds upon Goldstein’s formulation of the FW-H equation for moving media and describes the noise radiation to a field point as:
Where denotes the ambient sound speed, represents the acoustic density, t is observer time, and is ambient fluid density. The source time and coordinates are defined by and , respectively. indicates a time period encompassing all noise contributions, and is the area of the blade. Three terms on the right-hand side of Equation 1 correspond to the thickness, loading, and quadrupole noise components of the acoustic radiation.
The experimental data was from the measurements of an isolated DJI-9450 rotor by Zhou et al. [15]. The directivity of the noise at the first BPF, which is 180 Hz, was measured at five microphones that are positioned in a circle spanning from −45° to 45° with 1.2 m (i.e., 5 times the rotor diameter) away from the rotor. As shown in Figure 8, the present LES results for the first-BPF directivity agree with the experimental data, while showing discrepancies by approximately 1 dB as compared to the theoretical model in Equation 1. Thereby, the validity of the present simulation method is demonstrated.
FIGURE 8
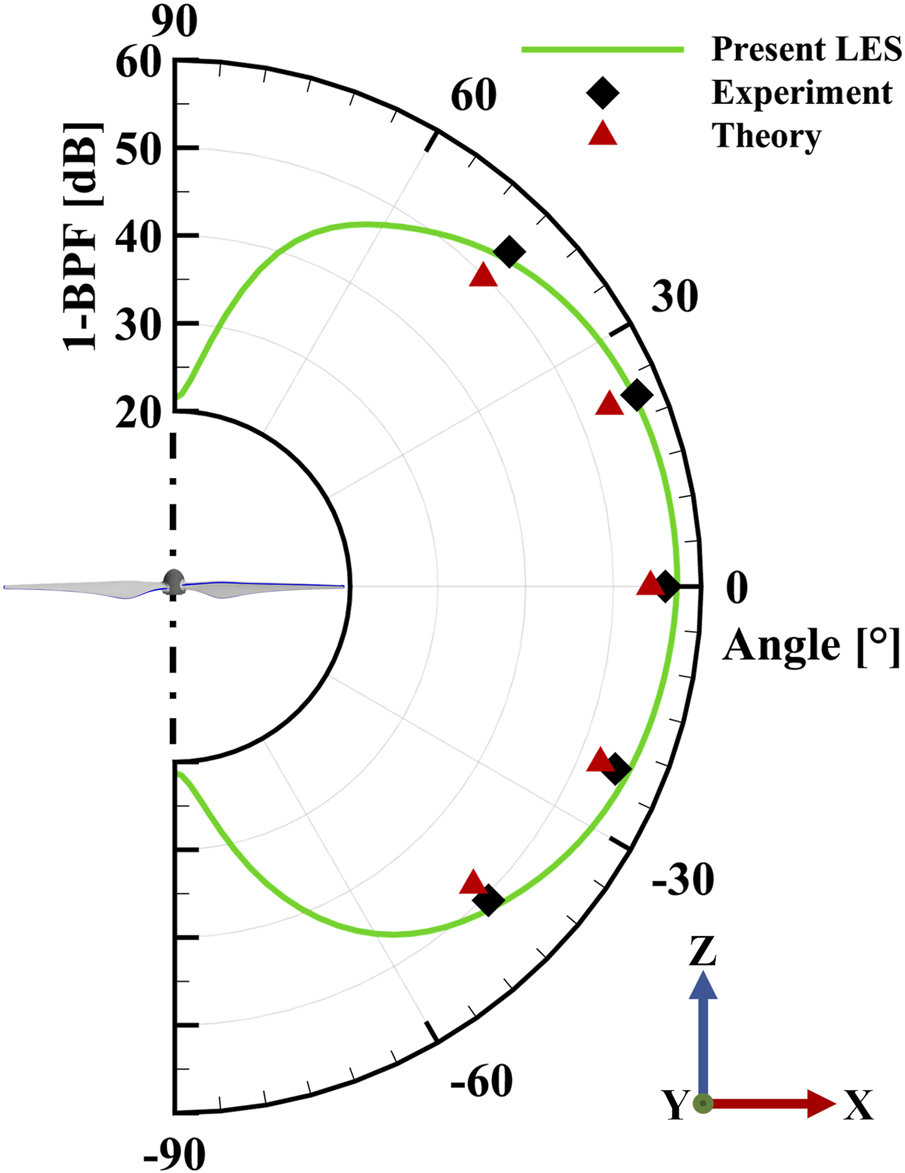
The directivity of the noise at the first BPF generated from the isolated rotor.
Near-Field Flow Characteristics
Figure 9 presents vortex isosurfaces, defined by the Q-criterion, for the two dual-rotor systems. In the case without a phase difference (°), the wakes from the rotors interact with each other in the middle position between them. This interaction is directly related to the phase change, so that the most intensified interaction happens when the blade tips have the shortest distance. In contrast, the case with ° shows less interaction of tip vortices in the region between the rotors.
FIGURE 9
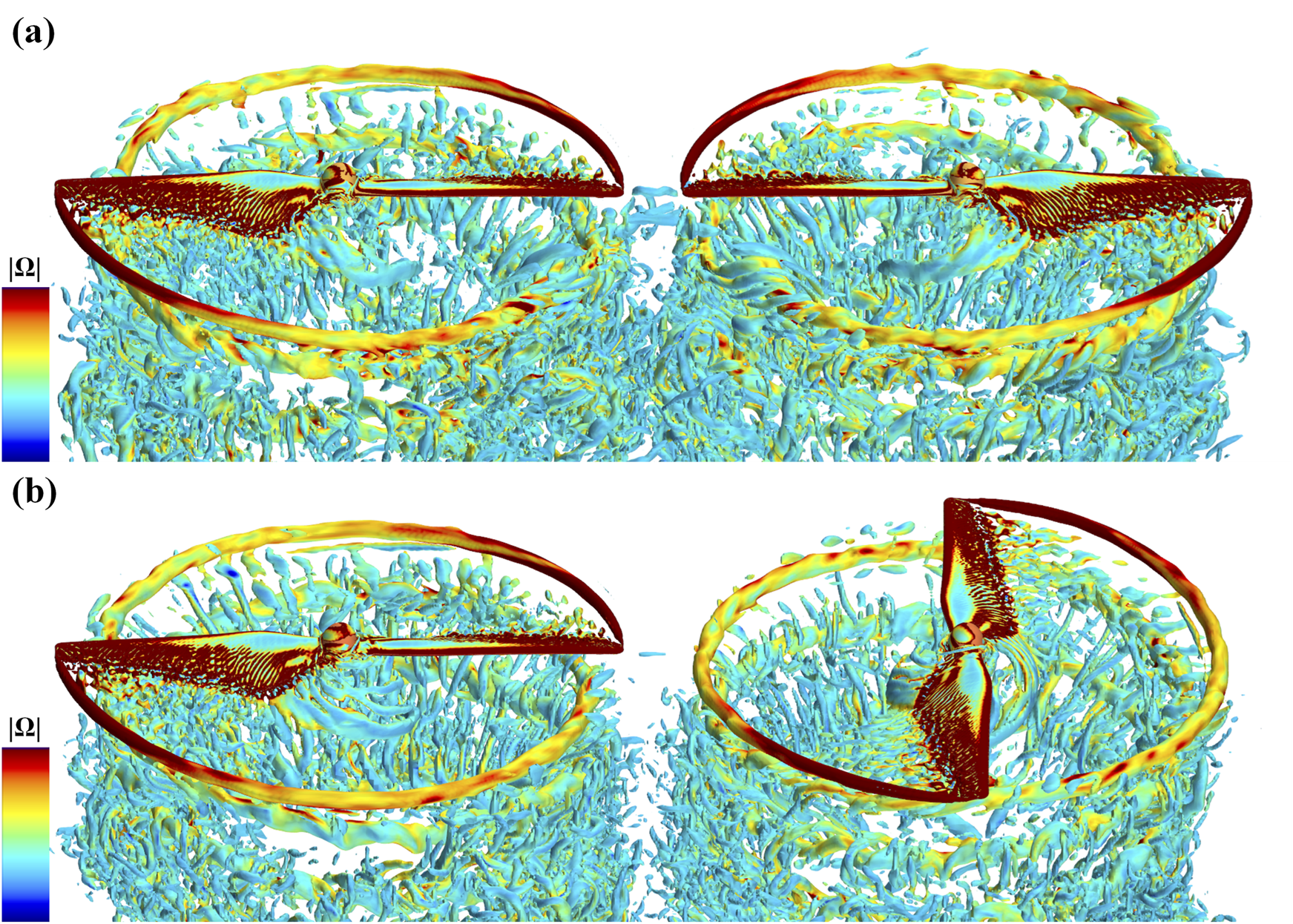
Vortices visualized through the Q-criterion (/s2) colored by vorticity magnitude (Max:5000/s, over 5000 shown in red) for (a)° and (b) °.
Vorticity magnitudes of the two dual-rotor systems are shown in Figure 10. In the case without a phase difference, tip vortices in the wake become unstable and dissipate rapidly. This might lead to the unsteady loads acting on the rotor tip and, consequently, increase the noise generation. In the case with the 90° phase offset, vortices in the zone between the rotors are relatively less turbulent, and tip vortices maintain their coherent patterns. This suggests that the wake interaction is weaker as compared to the other case.
FIGURE 10

Vorticity magnitudes (Max:5000/s, over 5000 is shown in red color) in the vertical cut-plane for (a)° (a) and (b) °.
Acoustic Pressure Counteracting Effect
The microphone positions for collecting acoustic pressure are illustrated in Figure 11. The microphones were set up along a circle with a radius of 2 times the rotor diameter. The circle center was positioned at the origin of the global coordinate system, which is in the middle of the gap between the two rotors. The circle is in the XY plane, in which the rotation centers of the rotors are located.
FIGURE 11
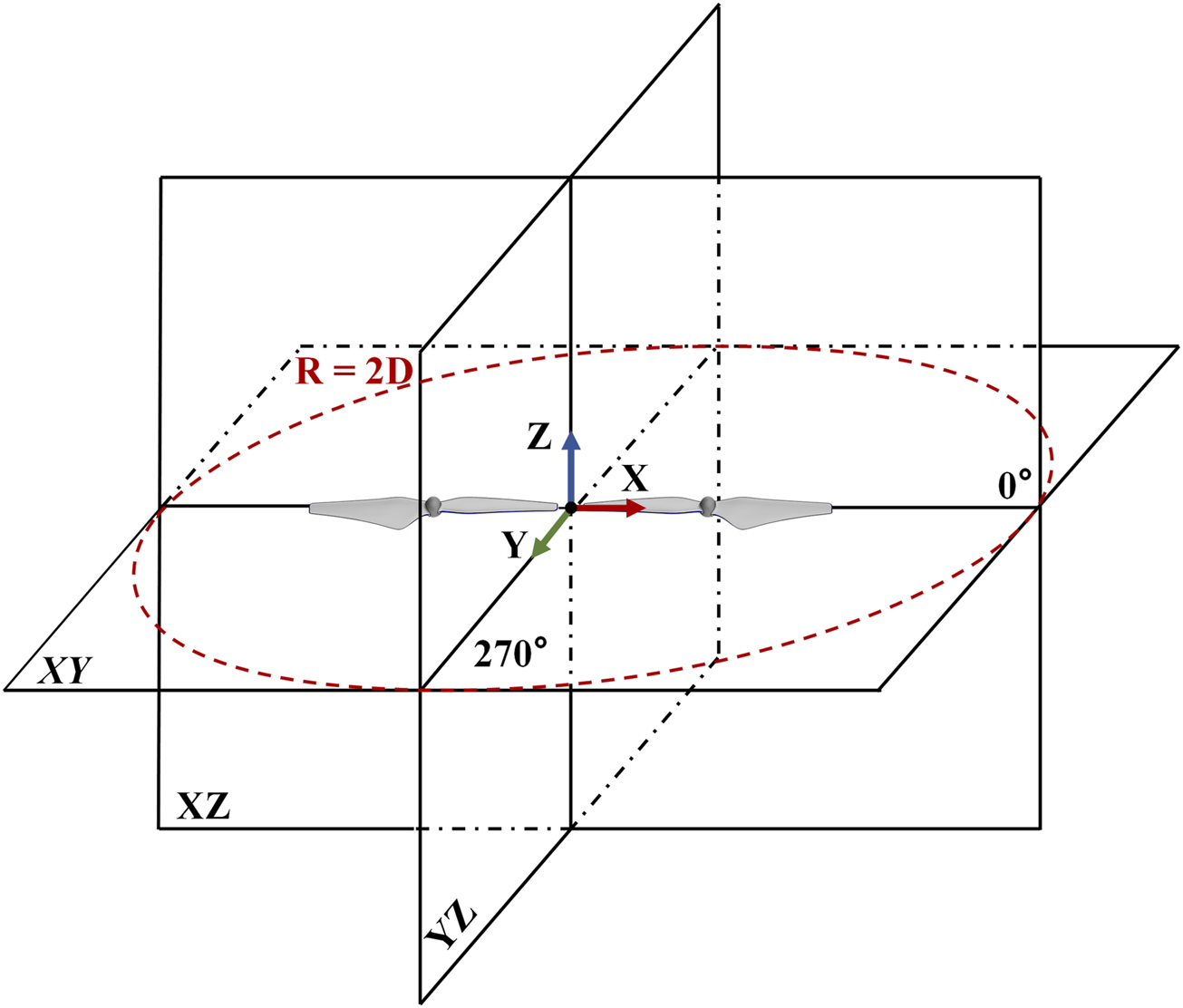
Locations of the microphones for monitoring acoustic pressure.
The time histories of acoustic pressure at the receiver of °, which are generated from each rotor and both of them in the case of °, are shown in Figure 12. It is evident that the acoustic pressure of each rotor shows periodic large-amplitude fluctuations, which are associated with the first BPF. However, the phases of the fluctuations between the two rotors exhibit a half-period difference. As a result, the total acoustic pressure from the sum of the two rotor’s acoustic pressure is significantly smaller and only contains high-frequency fluctuations, which are mostly related to the broadband component of the noise. This indicates a counteracting effect in the noise propagation.
FIGURE 12
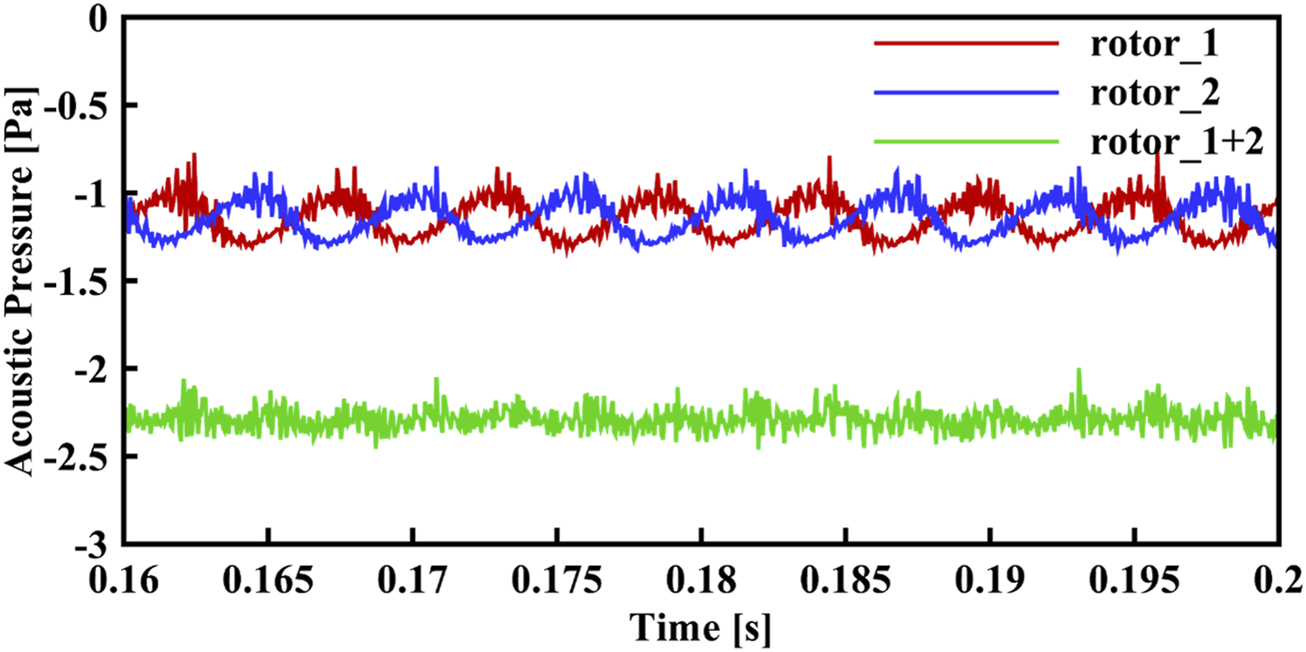
Time history of acoustic pressure at the microphone of ° in the dual-rotor case of °.
Directivity of Noise Propagation
The directivities of overall sound pressure levels (OASPL) in the vertical and horizonal directivities, computed for each rotor and the whole dual-rotor system, are plotted in Figure 13. Here the horizontal directivities in the XY plane, vertical directivities are in the XZ and YZ planes. In the case without the phase difference (°), the total noise is larger than that from a single rotor in most vertical directions. However, when the phase difference is imposed, the total noise levels are smaller than every single rotor. This effect is more significant in the ZY plane.
FIGURE 13
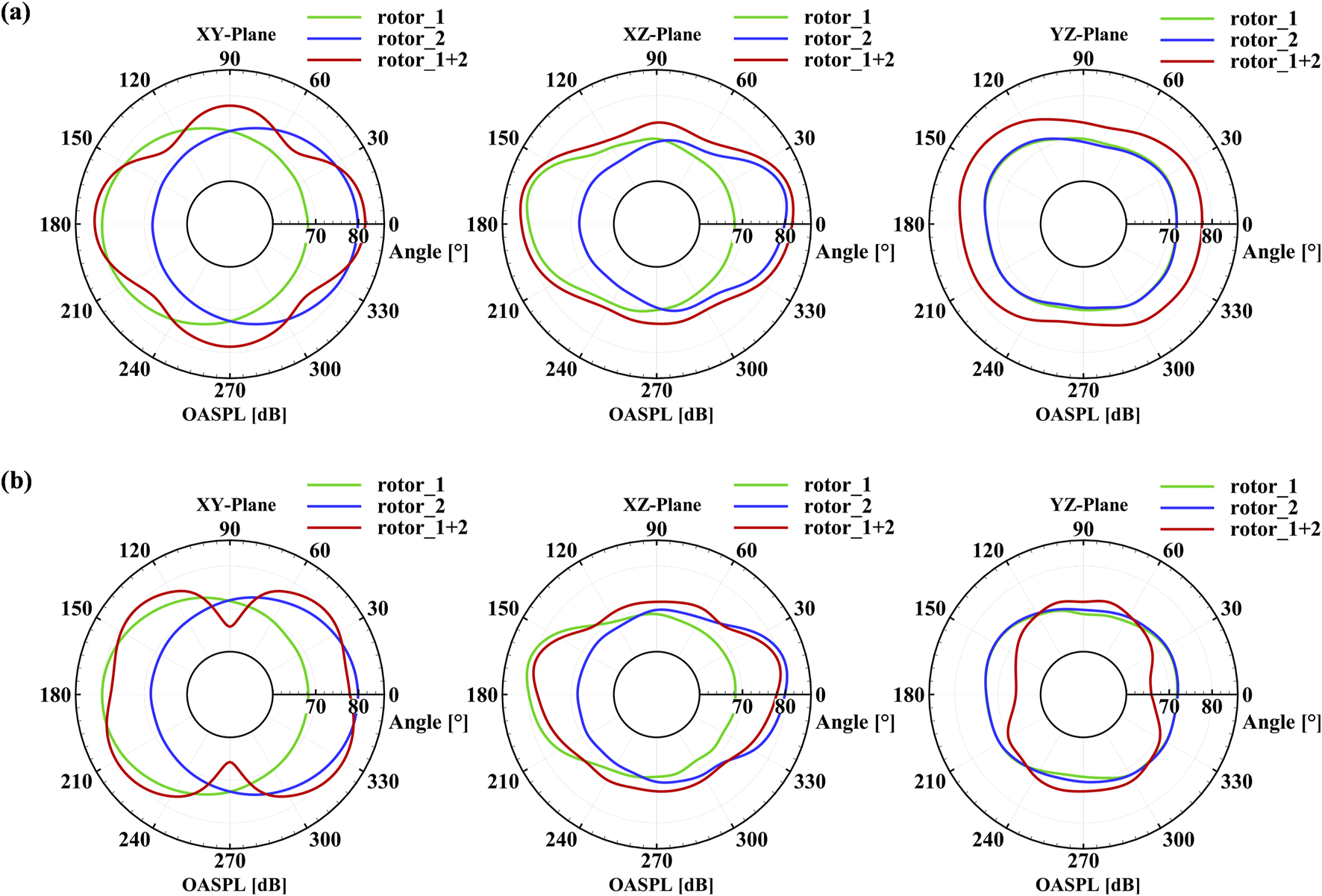
The noise directivity of (a)° and (b)°. From left to right: the horizontal XY plane, and the vertical XZ and YZ planes.
The OASPL of the total noise from the dual-rotor systems are compared in Figure 14. A maximum reduction of 10 dB is seen in the XY plane at the direction of °. The reason is that the polar pattern is changed from a quadrupole shape to a dipole shape, and that the largest polars point to the horizontal directions. Additionally, the total noise in the XZ and YZ planes is also attenuated significantly when the phase difference is set.
FIGURE 14
![Polar plots of OASPL [dB] for different planes: XY-Plane, XZ-Plane, and YZ-Plane. Each plot shows two lines, blue for phi equals zero degrees and red for phi equals ninety degrees, indicating the distribution of sound levels across angles from zero to three hundred sixty degrees.](https://www.frontierspartnerships.org/files/Articles/15262/xml-images/arc-03-15262-g014.webp)
The directivities of the total noise.
Discussion
Discussion of Noise Mapping
Noise maps of A-weighted OASPL in planes, which are positioned at a distance of 10D from the center of the dual-rotor system, are shown in Figures 15a,b. Here D denotes the rotor diameter. To construct the noise maps, far-field observers for collecting sound pressure were distributed at points that constitute structured grids with uniform spacing in the planes. For instance, in the plane at Z = −2.4 m, a rectangular area of 4.8 m × 4.8 m was discretized using a grid of 20 × 20, resulting in 400 observers with the grid spacing of 0.24 m, which is one rotor diameter. Similarly, structured grids were set for the other planes. Based on the grid topology, contours of sound pressure levels can be established in the far field.
FIGURE 15
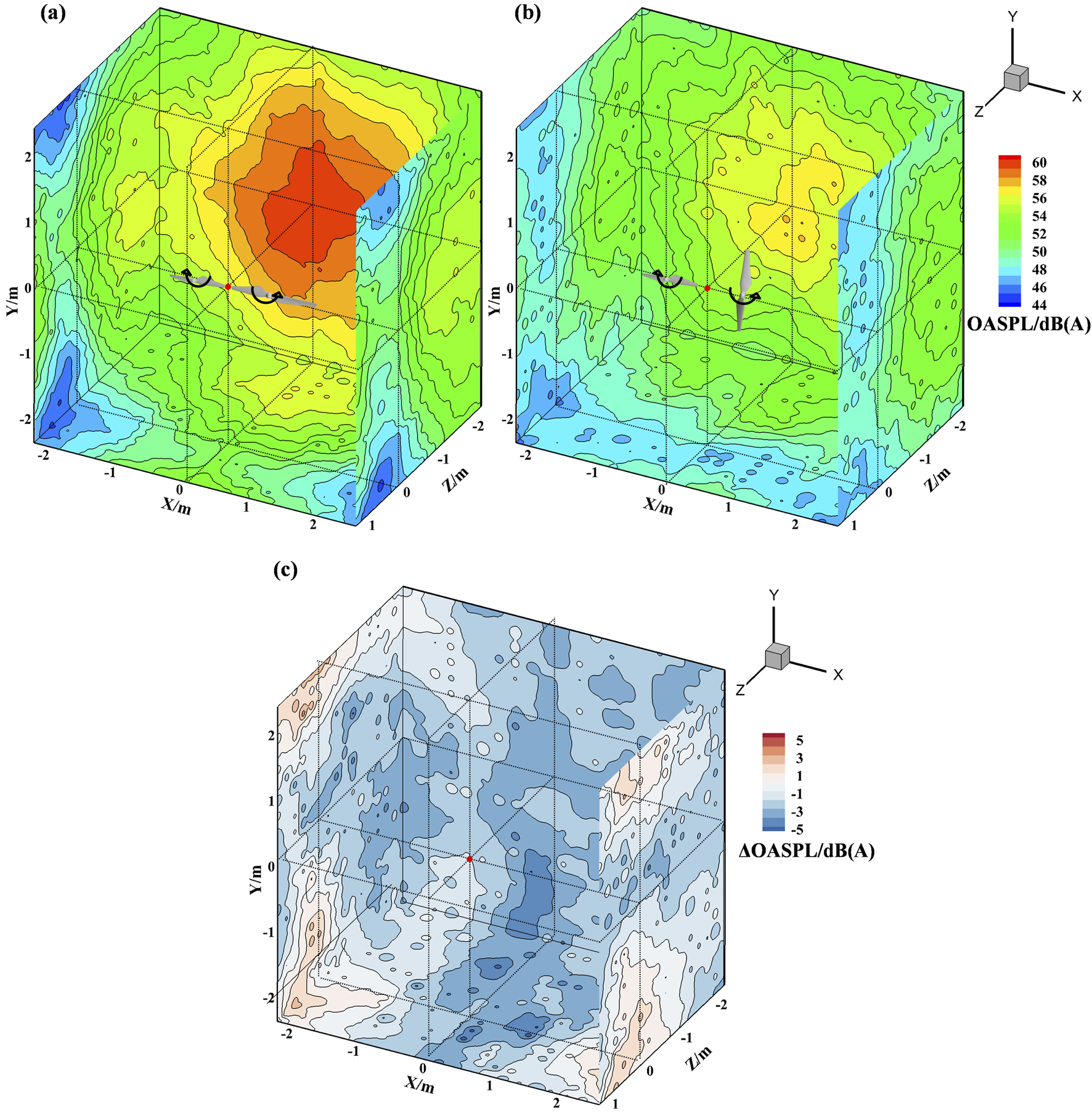
Noise maps in the far field with 10D from the center of the dual-rotor system. (a)°, (b)°, (c) OASPL.
In the case without the phase difference, noise levels are around 54 dB(A) in the vertical directions towards the ground. A significant large noise region is seen in horizontal directions, which are not highly concerned since the noise will not directly propagate to the ground and affect the residence. On the other hand, in the same vertical and horizonal regions, the phase difference results in lower noise levels. Near the corner regions where the noise propagation directions are oblique to the ground, the noise levels are increased due to the phase difference. But the noise is still fairly small around 46 dB(A) compared to other directions, meaning insignificant noise pollution.
The values of A-weighted OASPL, calculated by subtracting the 0-deg results from the 90-deg results, are shown in Figure 15c. As can be seen, the phase difference leads to noise reduction up to 5 dB(A) in directions vertical to the ground plane, where the original noise levels (without the rotor phase difference) are large. Compared to the near-field directivity (at a distance of 2D in Figure 14), the noise reduction in the downstream negative Z direction is more pronounced. Since acoustic interference effects in the near field are still developing, the far-field directivity has not yet been fully established. In contrast, for the far-field noise map (Figure 15) at a distance of 10D, wave propagation and coherent cancellation effects become more evident. As sound propagates, constructive and destructive interference patterns grow distinct, leading to significant noise reduction in specific directions particularly vertically downward toward the ground. Although noise levels increase by 3∼4 dB(A) in directions oblique to the ground, the resultant noise is low (see Figure 15a) since the original levels at the same positions are insignificant (see Figure 15b).
Conclusion
In this study, a numerical investigation was conducted to analyze the phase-synchronization of a quarter of the rotation period (°), to reduce noise generated from a DIJ-9450 dual-rotor system under the hovering condition. The numerical method was LES for the flow simulation integrated with the FW-H acoustic analogy for the noise prediction. The sliding mesh approach was employed to account for the rotor motions. This study focuses on the 90° phase difference as a typical case, whose noise reduction mechanism essentially lies in controlling the relative motion phase between the two rotors, thereby altering the coherence characteristics of the radiated sound waves during far-field propagation and generating directional destructive interference of sound pressure. This mechanism is universally applicable to various phase configurations: although the optimal phase angle for a specific system may vary depending on factors such as rotor geometry, rotational speed, and observer position, the underlying principle of acoustic interference based on phase modulation remains broadly generalizable.
While this study is conducted using the DJI-9450 rotor, the fundamental physical mechanisms involved, such as tip vortex interactions and acoustic pressure wave cancellation are universal in nature. Although specific rotor geometries, including the number of blades, twist distribution, and diameter, may affect the optimal phase angle and the magnitude of noise reduction achievable, the principle of noise cancellation through phase control remains broadly applicable across different rotor configurations.
The results indicate that phase synchronization significantly alters the spatial pattern of the noise propagation in the far field. The 90° phase difference between the two rotors weakens interactions of tip vortices induced by the blades. Furthermore, a phase counteraction of the noise between the rotors is introduced, resulting in obvious tonal noise reduction at the BPF in the noise propagation directions normal to the ground, which are of high important in the real-world UAM. By plotting noise maps in a distance of 10 times the rotor diameter, it was found that the A-weighted OASPL was reduced up to 5 dB(A) in the region underneath the dual rotors, namely, the noise propagation directions normal the ground plane. In the region, the original noise levels without the rotor phase difference (°) are large. The noise in side regions is increased by 3∼4 dB(A), but this is not important since the final noise levels in these regions are still small given the original low levels.
Overall, the study demonstrates that the phase synchronization is potentially an effective strategy for directional noise mitigation in dual-rotor systems. It explores phase-synchronized noise reduction for eVTOL dual-rotor systems in hover. It employs how phase differences affect vortex interactions and acoustic directivity. It is based on established LES and FW-H acoustic analogy techniques, their application to this specific context yields quantitative and mechanism-rich conclusions, demonstrating evident novelty. Nevertheless, the mitigation is space-dependent, and a universal mitigation across all directions in the noise propagation is challenging and this control method imposes higher requirements on phase control accuracy and multi-rotor coordinated control. Future work will extend the analysis to include the influence of forward flight conditions, actuator control precision, installation effects, and phase matching errors into dual- or multi-rotor systems. The research is expected to provide fundamental guidance and technical support for eVTOLs and other types of UAM vehicle in real operational environments.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
ZC is responsible for the values simulation, data processing, and manuscript writing. XL is responsible for research guidance and manuscript review. H-DY is responsible for simulation guidance and manuscript review. All authors contributed to the article and approved the submitted version.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
References
1.
Goyal R Reiche C Fernando C Serrao J Kimmel S Cohen A et al Urban Air Mobility (UAM) Market Study. NASA Technical Publication (2018). Available online at: https://ntrs.nasa.gov/citations/20190001472 (Accessed July 12, 2025).
2.
Silva C Johnson WR Antcliff KR Patterson MD . VTOL Urban Air Mobility Concept Vehicles for Technology Development. AIAA Aviation 2018 Forum (2018). 10.2514/6.2018-3847
3.
Rizzi SA Huff DL Boyd DD Bent P Henderson BS Pascioni KA et al Urban Air Mobility Noise: Current Practice, Gaps, and Recommendations. NASA Technical Publication (2020). Available online at: https://ntrs.nasa.gov/citations/20205007433 (Accessed July 12, 2025).
4.
Kim JH . Urban Air Mobility Noise: Further Considerations on Indoor Space. Int J Environ Res Public Health (2022) 19(18):11298. 10.3390/ijerph191811298
5.
Lee W Kim Y Jeong J Lee S . Partial Loudness-Based Perceptual Noise Analysis of Multirotor Type Urban Air Mobility VTOL. J Mech Sci Technology (2025) 39(1):35–46. 10.1007/s12206-024-1204-8
6.
Johnson W Silva C Solis E . Concept Vehicles for VTOL Air Taxi Operations. In: AHS Specialists’ Conference on Aeromechanics Design for Transformative Vertical Flight (2018).
7.
Kim H Lee J Lee D Yee K . Improved Conceptual Design of eVTOL Aircraft: Considering Rotor–Rotor Interactional Effects. Int J Aeronaut Space Sci (2025) 26(2):863–82. 10.1007/s42405-025-00888-9
8.
Intaratep N Alexander WN Devenport WJ Grace SM Dropkin A . Experimental Study of Quadcopter Acoustics and Performance at Static Thrust Conditions. 22nd AIAA/CEAS Aeroacoustics Conf (2016). 10.2514/6.2016-2873
9.
Turhan BB Jawahar HK Rezgui D Azarpeyvand M . Characterizing the Noise Patterns of Overlapping Propellers in Forward Flight. The J Acoust Soc America (2025) 157(4):2790–801. 10.1121/10.0036453
10.
Mukherjee B Brentner KS . Investigation of Propeller-Wing Interaction Noise and the Potential Contribution to eVTOL Noise. Aeromechanics for Advanced Vertical Flight Technical Meeting. San Jose: Vertical Flight Society (2020). p. 78–92.
11.
Afari S Golubev V Lyrintzis AS Mankbadi R . Review of Control Technologies for Quiet Operations of Advanced Air-Mobility. Appl Sci (2023) 13:2543. 10.3390/app13042543
12.
Schiller NH Pascioni KA Zawodny NS . Tonal Noise Control Using Rotor Phase Synchronization. Vertical Flight Soc Annu Forum & Technology Display (2019) 1–12. 10.4050/F-0075-2019-14455
13.
Guan S Lu Y Su T Xu X . Noise Attenuation of Quadrotor Using Phase Synchronization Method. Aerospace Sci Technology (2021) 118:107018. 10.1016/j.ast.2021.107018
14.
Hertzman O Fligelman S Stalnov O . Abatement of a Multi-Rotor Tonal Noise Component with Phase Control Technology. In: 28th AIAA/CEAS Aeroacoustics Conference. (Haifa: American Institute of Aeronautics and Astronautics Inc.) AIAA-2022-2834 (2022). 10.2514/6.2022-2834
15.
Zhou T Fattah R . Tonal Noise Acoustic Interaction Characteristics of Multi-Rotor Vehicles. In: 23rd AIAA/CEAS Aeroacoustics Conference (2017). AIAA-2017-4045. 10.2514/6.2017-4054
16.
Shao M Lu Y Xu X Lu J . Experimental Study on Noise Reduction of Multi-Rotor by Phase Synchronization. J Sound Vibration (2022) 539:117199. 10.1016/j.jsv.2022.117199
17.
Joseph P Paruchuri C Elliott S Bhardwaj M Chong TP . Propeller Tonal Noise Reductions Through Synchrophasing: Mechanisms and Performance. J Sound Vibration (2025) 610(1):119110. 10.1016/j.jsv.2025.119110
18.
Turhan B Jawahar HK Gautam A Syed S Vakil G Rezgui D et al Acoustic Characteristics of Phase-Synchronized Adjacent Propellers. The J Acoust Soc America (2024) 155(5):3242–53. 10.1121/10.0025990
19.
Yoon S Lee HC Pulliam TH . Computational Analysis of Multi-Rotor Flows. In: 54th AIAA Aerospace Sciences Meeting (2016). Paper AIAA-2016-0812. 10.2514/6.2016-0812
20.
Ventura Diaz P Yoon S . High-Fidelity Computational Aerodynamics of Multi-Rotor Unmanned Aerial Vehicles. In: AIAA Aerospace Sciences Meeting. (Kissimmee: American Institute of Aeronautics and Astronautics Inc.) Paper AIAA-2018-1266 (2018). 10.2514/6.2018-1266
21.
Alvarez EJ Schenk A Critchfield T Ning A . Rotor-On-Rotor Aeroacoustic Interactions of Multirotor in Hover. In: Vertical Flight Society 76th Annual Forum(Red Hook: Vertical Flight Society) (2020). 10.4050/F-0076-2020-16489
22.
Smith B Gandhi F Niemiec R . A Comparison of Multicopter Noise Characteristics with Increasing Number of Rotors. In: 76th Annual Forum of the Vertical Flight Society. F-0076-2020-16499 (2020). 10.4050/F-0076-2020-16499
23.
Simcenter STAR-CCM+, Version (2021.2). Siemens Digital Industries Software (2021).
24.
Thurman CS Zawodny NS Baeder JD . Computational Prediction of Broadband Noise from a Representative Small Unmanned Aerial System Rotor. Vertical Flight Soc Forum (2020) 76:1–9. 10.4050/F-0076-2020-16492
25.
Hanson DB Parzych DJ . Theory for Noise of Propellers in Angular Inflow with Parametric Studies and Experimental Verification. In: NASA contractor Report (Cleveland: NASA, Lewis Research Center). NASA-CR-4499 (1993). Available online at: https://ntrs.nasa.gov/citations/19930015905 (Accessed July 12, 2025).
Summary
Keywords
eVTOL, hover wake interaction, phase synchronization, tonal noise counteraction, dual-rotor system
Citation
Chai Z, Li X and Yao H-D (2025) Numerical Study on Dual-Rotor Phase Synchronization for Tonal Noise Counteraction. Aerosp. Res. Commun. 3:15262. doi: 10.3389/arc.2025.15262
Received
13 July 2025
Accepted
12 September 2025
Published
24 September 2025
Volume
3 - 2025
Updates
Copyright
© 2025 Chai, Li and Yao.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaodong Li, lixd@buaa.edu.cn
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.