Abstract
The thermal cloak has special thermal insulation performance because of its unique anisotropic thermal conductivity tensor. Constrained by simplistic geometric designs, traditional thermal cloaks face limitations in achieving precise thermal regulation for complex structures with different shapes. The hexagonal and dodecahedral thermal cloaks are quite rare, largely due to their complex transformation equations. In this study, the transformation equations for the hexagonal and dodecahedral cloaks are derived by the rotation matrix, and their thermal conductivity tensors are further obtained according to the theory of transformation thermotics. The derivation method is applicable to any two and three-dimensional thermal invisibility cloaks with geometric symmetry. Furthermore, the numerical verification shows that both hexagonal and dodecahedral thermal cloaks could avoid heat flow in their thermal invisibility region. This proves the correctness of the derivation method and the thermal conductivity tensor calculated. The hexagonal and dodecahedral thermal cloaks obtained in this paper could provide uniform temperature field for different applications preventing the field of non-uniform stress and deformation in actual.
Introduction
Thermal metamaterials make it possible to actively manipulate heat phenomena of artificial systems and govern heat diffusion processes [1]. Various thermal metamaterials with different functionalities have already been demonstrated due to the development of transformation thermotics [2]. Thermal cloak, as one of the thermal metamaterials, provides a zero-temperature gradient inside a central region without disturbing the temperature distribution in the surrounding region. So, such cloak is of an application in hiding or protecting objects from being detected or destroyed [3]. The thermal cloaks have been extensively studied since Pendry et al. [4] designed an artificial metamaterial based on the formal invariance of Maxwell’s equation and achieved electromagnetic invisibility. Fan et al. [5] introduced the concept of electromagnetic cloak into the thermal field for the first time and predicted the thermal invisibility cloak theoretically. Narayan et al. [6] synthesized two materials with very different thermal conductivity into a spiral multilayer structure and made a prototype of a thermal cloak. Various cloak has been studied, such as the bifunctional cloak [7], switchable thermal cloak [8] and the microstructured thermal cloak [9]. Realizing anisotropic thermal conductivities as expected is essential for thermal cloak. Jian Z et al. [10] found that periodic dimpling of silicon film could reduce thermal conductivity and constructed a rectangular cloak in this way. Yang S et al. [11] proposed a single-particle structure to effectively manipulate the thermal conductivity by appropriately adjusting the form factor or area fraction of the single particle. Sha et al. [12] took the local thermal conductivity tensor as input, carried out the free form design of topological functional units by topology optimization, and then directly 3D printed and assembled them to design three free-form thermal devices. Ji et al. [13] propose a machine learning based thermal cloak consisting of a finite number of layers with isotropic materials. Han et al. [14] demonstrate the design of full-parameter omnidirectional thermal metadevices with anisotropic geometry, which is experimentally confirmed via three proof-of-concept experiments. Li et al. [15] suggest a de-homogenization approach that uses optimal multi-rank laminates to provide closed-form solutions for any imaginable thermal manipulation device and create thermal cloaks, rotators, and concentrators. A forward conformality-assisted tracing method is proposed, which uses a conformal mesh composed of orthogonal streamlines and isotherms to produces free-form metamaterials using only isotropic media [16]. At the microscopic level, how to adjust the thermal conductivity is also a research hotspot [17–20], which provides a new idea for the actual preparation of thermal invisibility cloak.
Hexagon has been used in elastic metamaterials [21] dual-band terahertz metamaterial absorber [22] and mechanical metamaterials [23]. Dodecahedron is one of the densest known packings of the non-tiling Platonic in three-dimensional Euclidean space [24]. The mechanical metamaterials [25] of dodecahedron is widely researched such as their topology-property relationships [26] and mechanical properties [27–32]. However, rare researchers have deduced the thermal insulation performance of hexagonal and dodecahedral thermal cloaks. In this study, the thermal conductivity tensors of hex-agonal and dodecahedral thermal cloaks are derived to provide uniform temperature field for different applications to prevent non-uniform stress and deformation from nonuniform heat flow in actual situation. The method in this paper could be applied to any two-dimensional or three-dimensional cloak with geometric symmetry.
Hexagonal Thermal Cloak
Derivation of the Hexagonal Cloak’s Thermal Conductivity Tensor
If there is no heat resource and at steady state, the heat conduction equation is:where represents the thermal conductivity of the medium, T is the temperature. Since the heat conduction equation has formal invariance [33], Equation 1 could be transformed in other space as Equation 2:where represent the thermal conductivity coefficients and temperatures in the transformed spaces. According to the theory of transformation thermotics [34], the relationship between transformation space and original space is:where A is the Jacobian transformation matrix, reflecting the geometric changes from the original space to the transformation space, and its components are:where denotes the three coordinate components x’, y’, z’ in the transformation space, represents the three coordinate components x, y, z in the original space.
Three steps would be carried out to obtain the thermal conductivity of the thermal cloak. Firstly, the geometric transformation equations of the cloak with complex shape should be established based on the rotation matrix which is obtained by the specific rotation method. Secondly, the Jacobian transformation matrix A could be formed according to the geometric transformation equations. Finally, the thermal conductivity coefficients of the cloak could be obtained by Equation 3.
The thermal conductivity tensor of hexagonal thermal invisibility cloak designed as Figure 1 is derived as follows. The cloak with anisotropic thermal conductivity tensors is set in the pink region so that the gray region in the middle is heat stealthy. The width of the hexagonal cloak and the middle invisibility region are and , respectively. Furthermore, the cloak is divided into six regions because of the geometric symmetry.
FIGURE 1
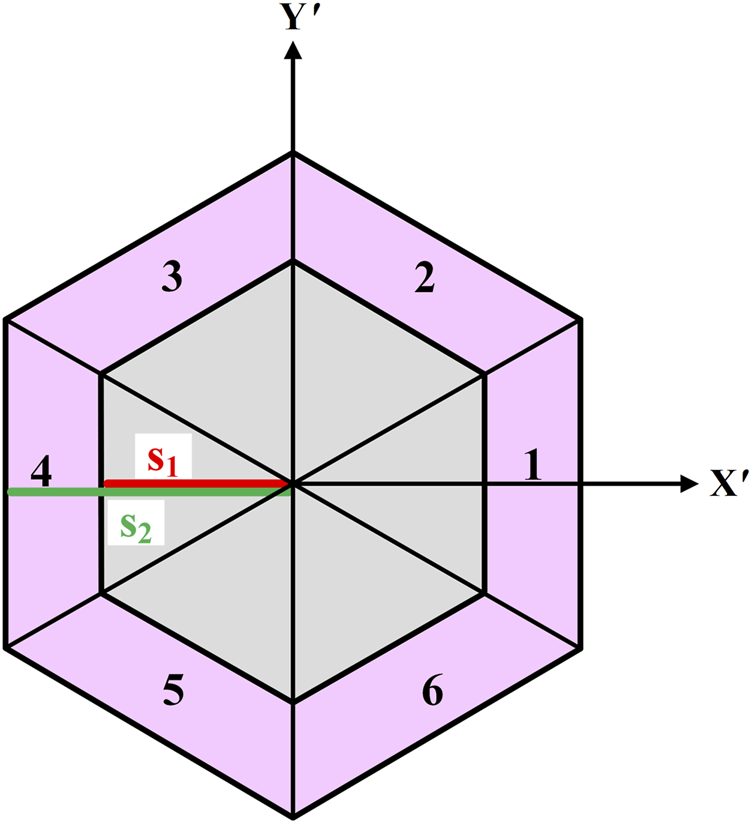
The sketch map of the hexagon thermal invisibility cloak (region ).
The transformation formula of region is easily established as Equation 5:
The corresponding Jacobian matrix of region could be calculated as Equation 6:
Then the thermal conductivity relationship of region between transformation space and original space is established as Equation 7 according to Equations 3, 6:
The region could be obtained by the rotating the region with 60° anticlockwise. The transformation equation of region could be set up by multiplying the transformation equation of region by the rotation matrix .
The corresponding Jacobian matrix and the thermal conductivity of region could be calculated as Equation 9 and Equations 10–13 according to Equations 3, 4, 8 as region :
In the same way, the left regions’ transformation equations could be established by multiplying the rotation matrix P in turn. Their Jacobian matrixes could be calculated. Finally, the thermal conductivities could be deduced as Equations 14–26.
Thermal Flux Insulation Numerical Verification of the Hexagonal Cloak
The correctness of the above thermal conductivity tensors of hexagonal thermal cloak will be verified directly in the numerical simulation. We take one example of the hexagonal thermal cloak model with , embedding in the square background filed with length of 60 m, which are established in the heat transfer module of the COMSOL Multiphysics software. For the hexagon with thermal cloak effects, the calculated thermal conductivity tensors of the cloak shell are input in the material properties setting module. The thermal conductivity coefficient of the original space , the background and the region inside the cloak are set to 1 to highlight the role of the derived anisotropic thermal conductivity tensor. Besides, the hexagon without thermal cloak effects, whose thermal conductivity coefficient of the whole region is 1 , is set as a comparison. The boundary conditions are set as 400 K for the left boundary and 300 K for the right boundary of the background. Other boundaries of the background are set to thermal insulation.
The distribution of temperature with heat flow lines and isotherms are shown in Figure 2. At the case of the hexagon with cloak effect, it could be seen in Figures 2A,C that the heat flows from the left boundary to the right boundary, parallel to each other in the background filed and concentrates in the cloak shell so that both the heat flow and the temperature gradient inside the cloak are zero because of the anisotropic thermal conductivity of the cloak shell. However, the heat flux passes through the whole hexagon without the cloak effect as Figure 2B and a gradient temperature is shown in Figure 2D. The temperature of the center line along the X-axis of the hexagon with and without the cloak is displayed in Figure 3, which further illustrated that the uniform temperature field inside the cloak with more obvious temperature gradient in the cloak shell region because of the hexagonal cloak effect. Both Figures 2, 3 demonstrate that the background temperature field remain consistent with the cloak effect or not. This is attributable to the fact that after the heat flux bypasses the cloak, it reverts to its original path in the external region of the cloak. This indicates that the hexagonal thermal cloak derived in this paper could effectively redirect heat flux without exerting influence on the background temperature field, which proves the correctness of the calculation method of the hexagonal thermal invisibility cloak and its thermal conductivity tensors.
FIGURE 2
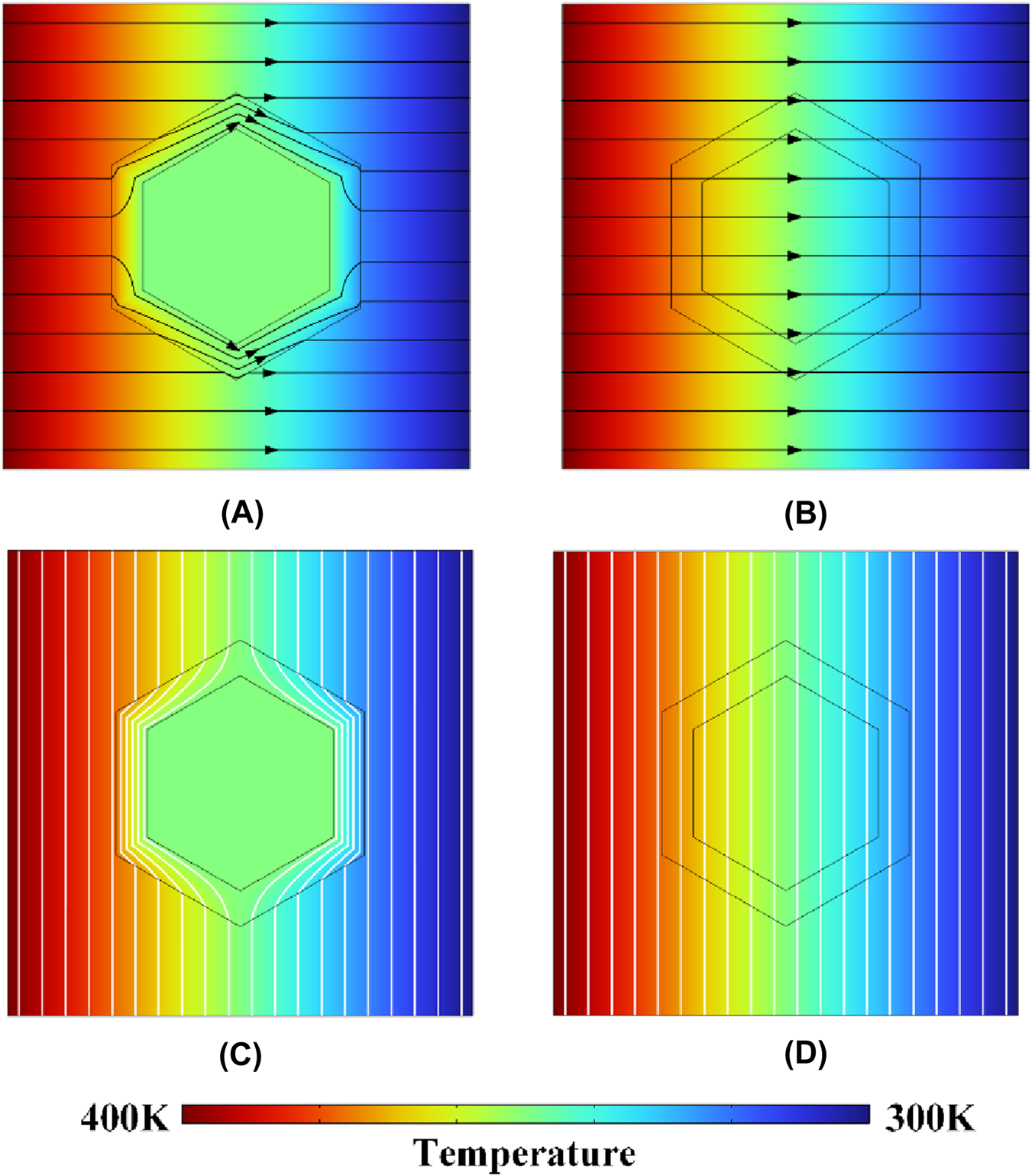
(A,B) The distribution of temperature and heat flow lines with and without the cloak effect. (C,D) The isotherms of the hexagon thermal cloak with and without the cloak effect.
FIGURE 3
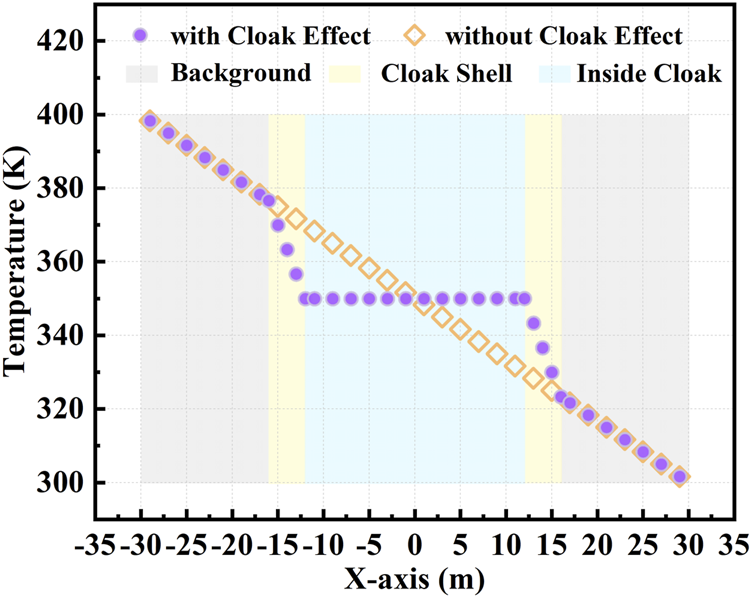
The temperature distribution on the center line along the X-axis of the hexagon with and without the thermal cloak effect.
Dodecahedral Thermal Cloak
Derivation of the Dodecahedral Cloak’s Thermal Conductivity Tensor
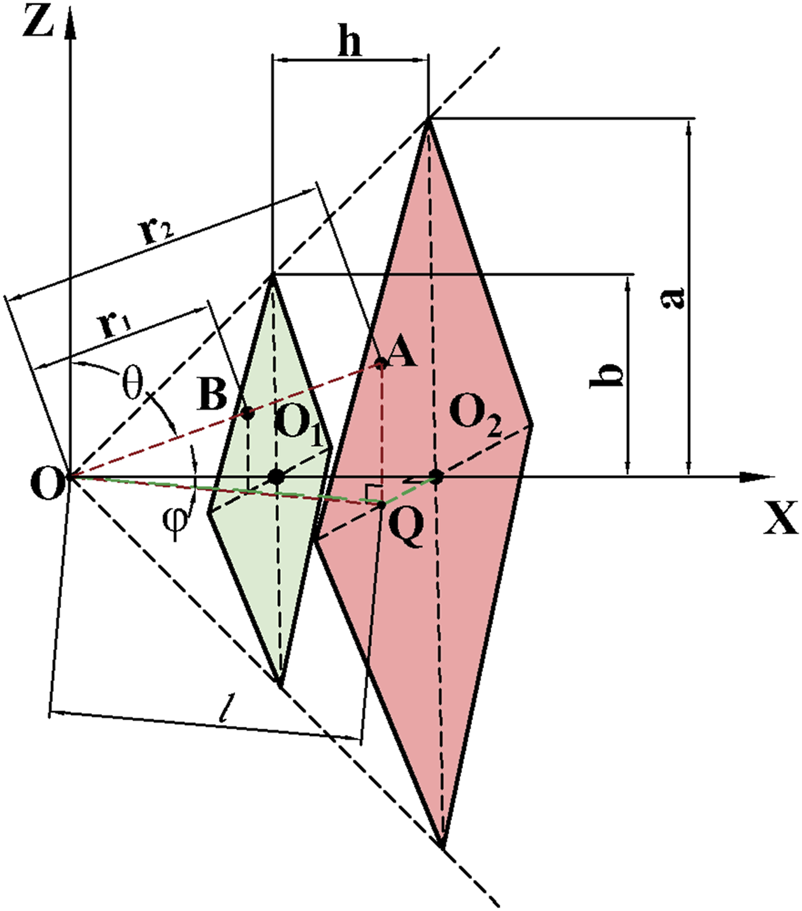
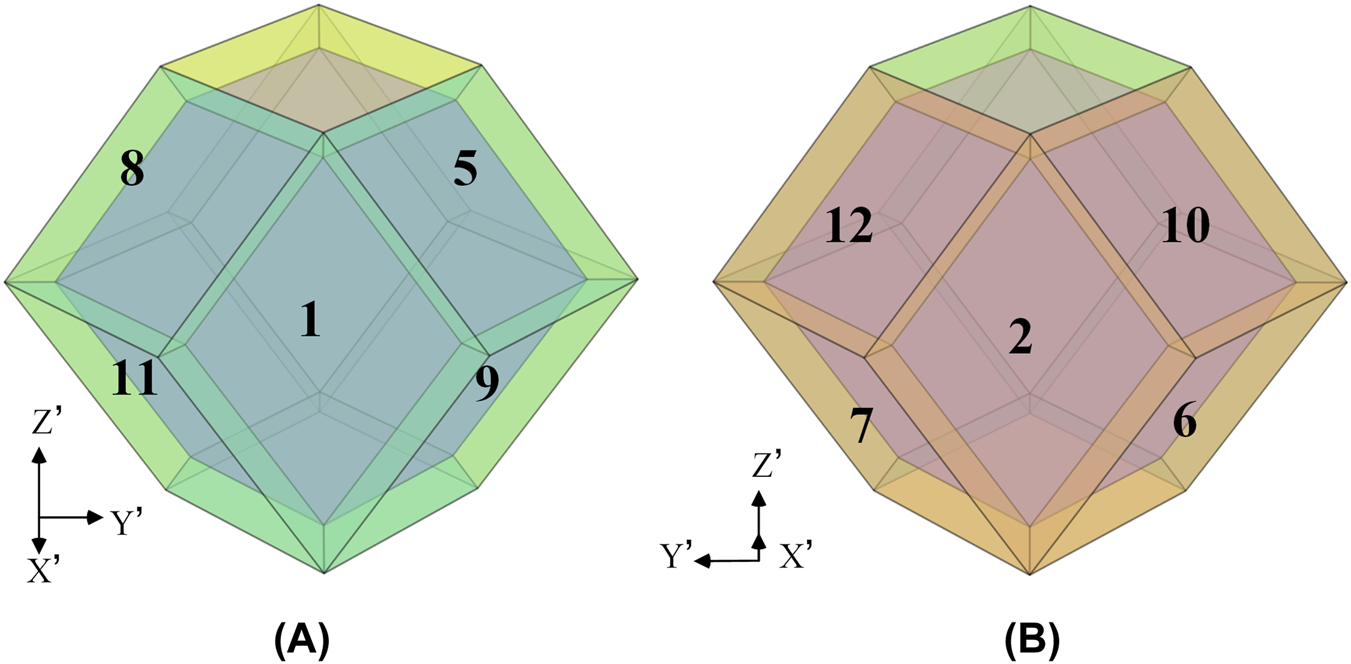
Different from the derivation of two-dimensional hexagonal thermal cloak, dodecahedron is a three-dimensional thermal cloak. Figure 4 illustrates the sketch map of rhombic dodecahedron thermal cloak. The rhombic dodecahedron thermal invisibility cloak is divided into 12 regions called as according to the symmetry. In Figure 4A, the regions marked in blue are facing us and the regions marked in orange are the faces facing away. Figures 4B,C are two facets of the cloak. The yellow shell indicates the cloak setting region and the purple region in the middle is the heat hiding region. The location of region is special which is parallel to the Y-Z plane and the X-axis passes through its midline point as Figure 5 shown.
FIGURE 4
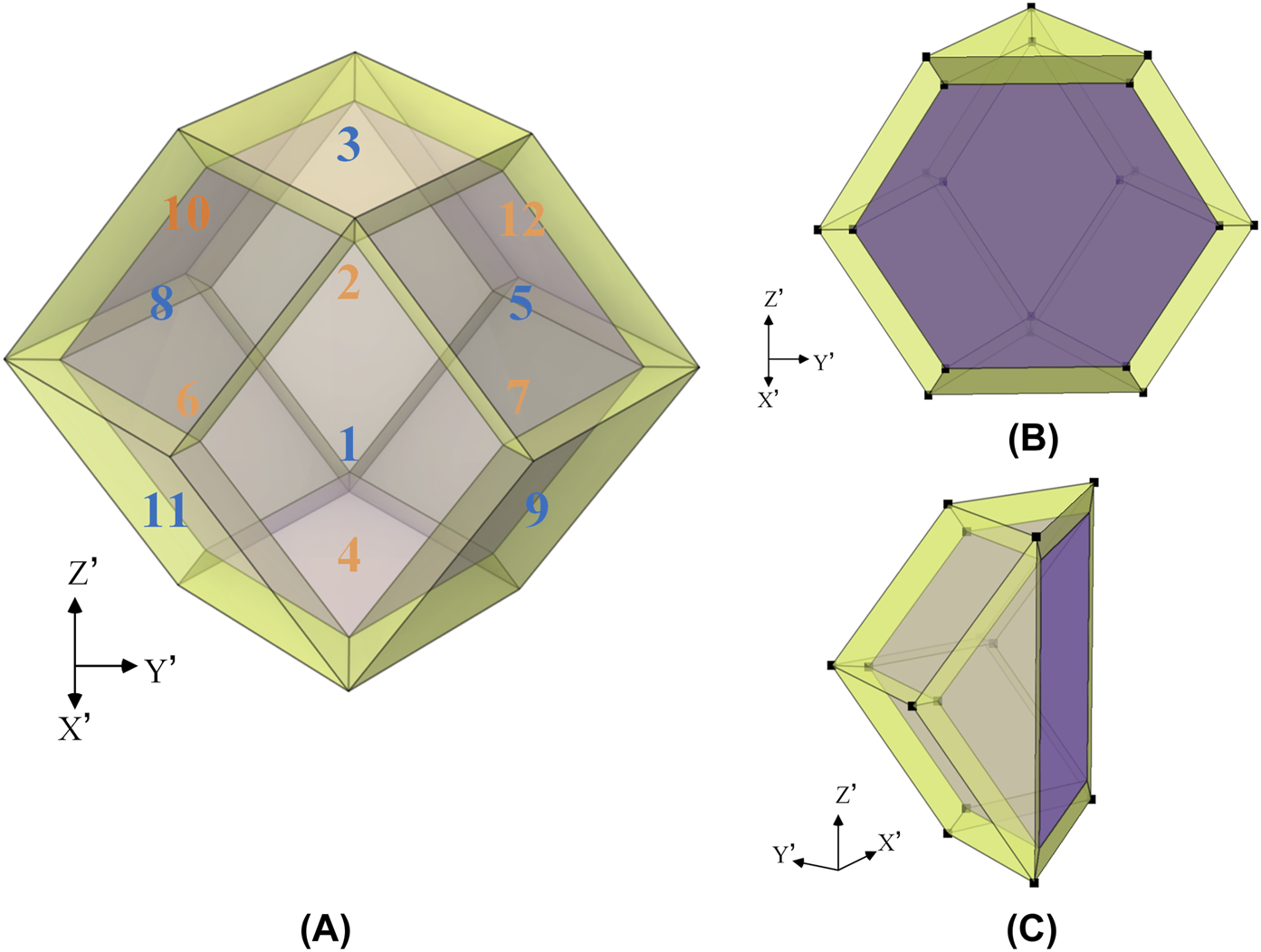
(A) The sketch map of the rhombic dodecahedron thermal invisibility cloak (region ). (B,C) are two facets of the cloak.
FIGURE 5
The schematic diagram of region of the rhombic dodecahedron cloak.
The green and pink diamonds represent the inner boundary and outer boundary of the rhombic dodecahedron thermal cloak in region , respectively. In triangles and , Equation 27 is obtained by trigonometric functions:
Therefore, the inner and outer boundaries of region could be expressed as Equation 28:
For a three-dimensional heat cloak, the transformation equation of compressing region into region is Equation 29:
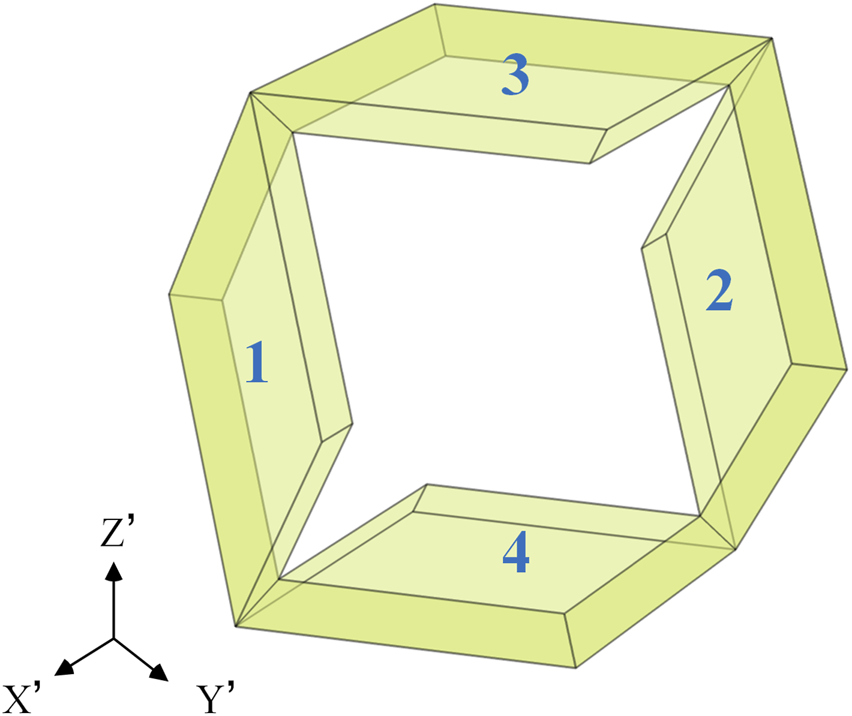
The region is chosen as the minimum rotation element because the transformation equation of it is easily to set up in Cartesian coordinates:
The transformation equations of region , , could be set up by rotating the region clockwise about the Y-axis with as Figure 6 noted. Using region as an example, the transformation equation of region could be calculated by multiplying Equation 30 by the relevant rotation matrix as Equation 31:
FIGURE 6
The schematic diagram of region .
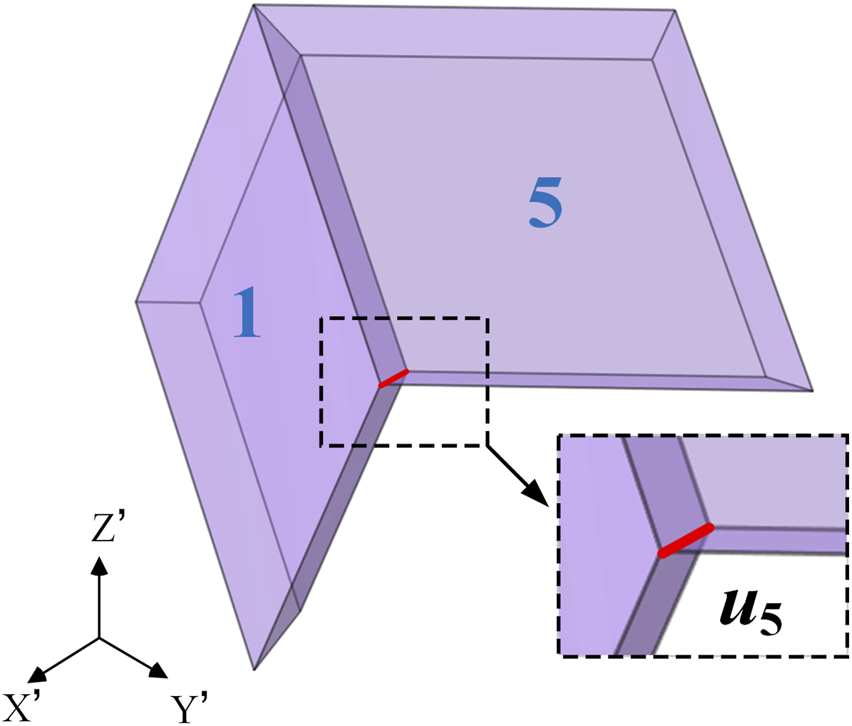
The rotation of the remaining regions is more special, no longer around the axis. They are divided into two categories, one by region rotation as Figure 7A shown, and the other by region rotation as Figure 7B. Use region as an example. The axis of the rotation of region is an edge of region , as Figure 8 shown. The region could be got by rotating region with 120° clockwise about the specified axis . The corresponding rotation matrix is . The transformation equations of region is Equation 32:where , .
FIGURE 7
(A) Regions , , , are obtained by rotating region . (B) Regions , , , are obtained by rotating region .
FIGURE 8
The rotation of region (the axis of rotation is marked in red).
In the similar way, the transformation equations of remain regions could be obtained by rotating the region and region with 120° counterclockwise or clockwise about their edges in the X-Y plane. Tables 1, 2 are the corresponding rotation axis and matrix of the region obtained by rotating region and region , respectively. Similarly, their Jacobian matrixes could be obtained by the transform equations. Finally, their thermal conductivity tensors could be calculated. The calculating progress is achieved by MATLAB.
TABLE 1
| Regions obtained by rotating region | Rotation axis | Rotation matrix |
|---|---|---|
| Region | ||
| Region | ||
| Region | ||
| Region |
The rotation axis and rotation matrix of the region obtained by rotating region .
TABLE 2
| Region obtained by rotating region | Rotation axis | Rotation matrix |
|---|---|---|
| Region | ||
| Region | ||
| Region | ||
| Region |
The rotation axis and rotation matrix of the region obtained by rotating region .
For the thermal cloak with less regular geometries or non-symmetric shapes, the present method is applicable too. For an any unregular region, the cloak could be divided into n sub-regions , which are no longer obtained by rotating the same “region ” that really exists. The “region ” of the sub-region could be set as a dummy region with the same shape of , and its position should be perpendicular or parallel to the coordinate axis to establish the transformation equations of easily.
Thermal Flux Insulation Numerical Verification of the Dodecahedral Cloak
The dodecahedral cloak with , embedding in a cube background, is established in the heat transfer module of the finite element software as Figure 9A shown. Taking the thermal conductivity of the original space , the middle stealth zone and the background as 1 , the calculated anisotropic thermal conductivity tensors of the dodecahedral cloak shell are set for the case of dodecahedron with cloak effect. For comparison, the dodecahedron without the cloak effects is considered by setting the thermal conductivity coefficient of the whole region is 1 . Set the upper and lower boundary of the background as 400 K and 300 K, respectively. Other boundaries are set to thermal insulation.
FIGURE 9
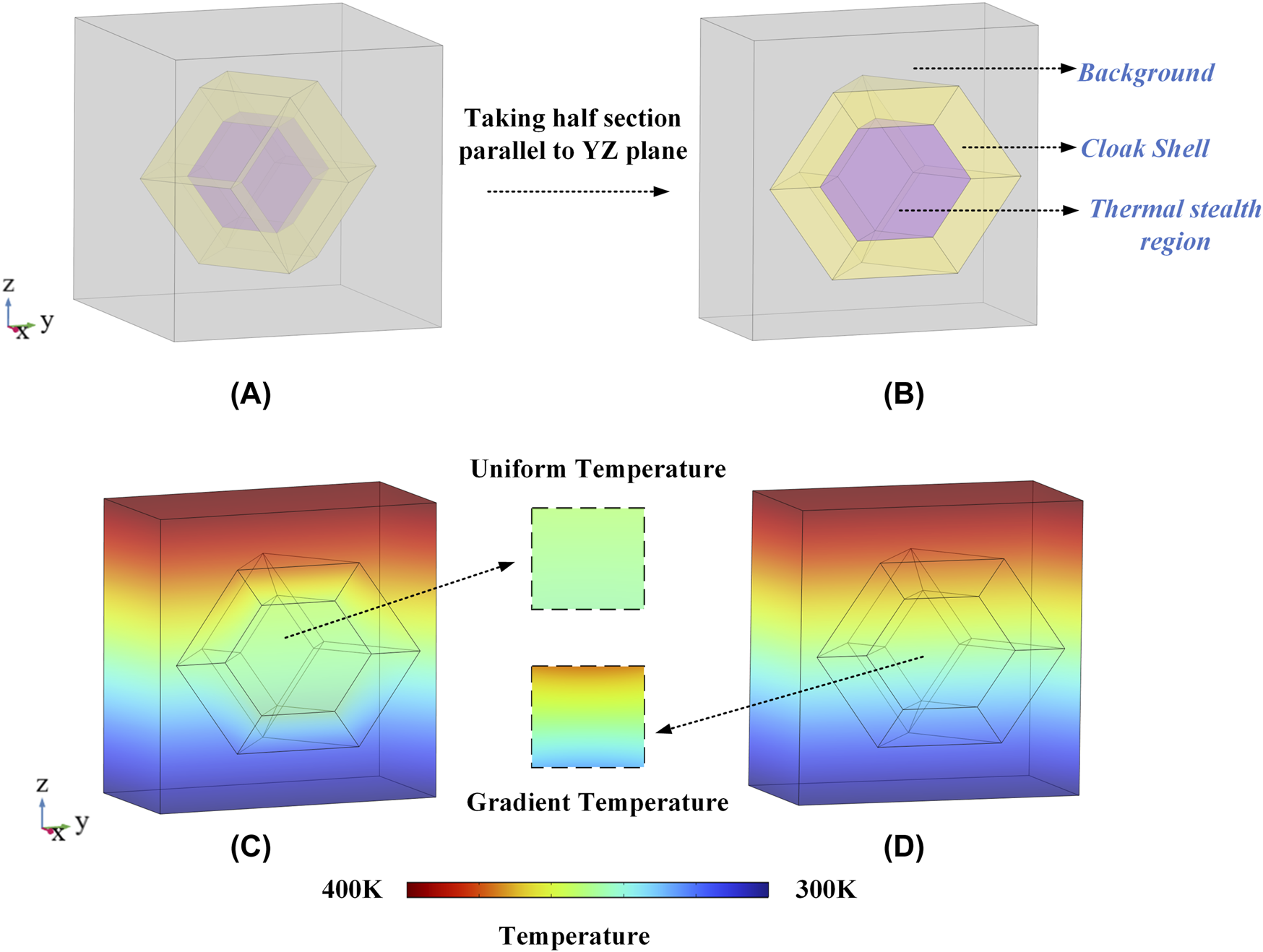
(A,B) The schematic diagram of the whole and half section of the rhombic dodecahedron thermal cloak with the background. (C,D) The half section’s temperature distribution of the background and the rhombic dodecahedron with the cloak or not.
The temperature distribution of the half section, which is taken parallel to YZ plane as Figure 9B, is given to facilitate the observation of the temperature distribution inside the rhombic dodecahedron thermal cloak. The uniform temperature filed is illustrated with the cloak effects in Figure 9C, which is different from the central gradient temperature without the cloak effects in Figure 9D.
The isothermal surface distribution of the rhombic dodecahedron with and without cloak effects is given in Figures 10A,B, respectively. Besides, Figures 10C,D show the temperature distribution of the rhombic dodecahedron’s tangent plane with and without the cloak. The temperature distribution on the center line of the rhombic dodecahedron and the background is illustrated in Figure 11. Without the heat cloak, it could be seen in Figure 10B that all isothermal surfaces are parallel to each other and the whole region is a gradient temperature filed from high to low. Figure 10A illustrates that the isothermal surfaces changes and buckle around the central invisibility region when the heat cloak is applied. The temperature gradient is concentrated at the cloak shell so the slope of the temperature line in the cloak setting region is greater than the absence of the cloak in Figure 11, and the central region in the dodecahedron is a uniform temperature field as Figure 10C shown. Moreover, in Figures 10, 11, the temperature filed of the background is identical whether the rhombic dodecahedron has the cloak effect or not, which proves that the dodecahedral thermal invisibility cloak doesn’t affect the background’s temperature filed. This proves that the dodecahedral thermal invisibility cloak plays a role in avoiding heat flow while the background filed isn’t disturbed, and the calculated thermal conductivity tensors are correct.
FIGURE 10
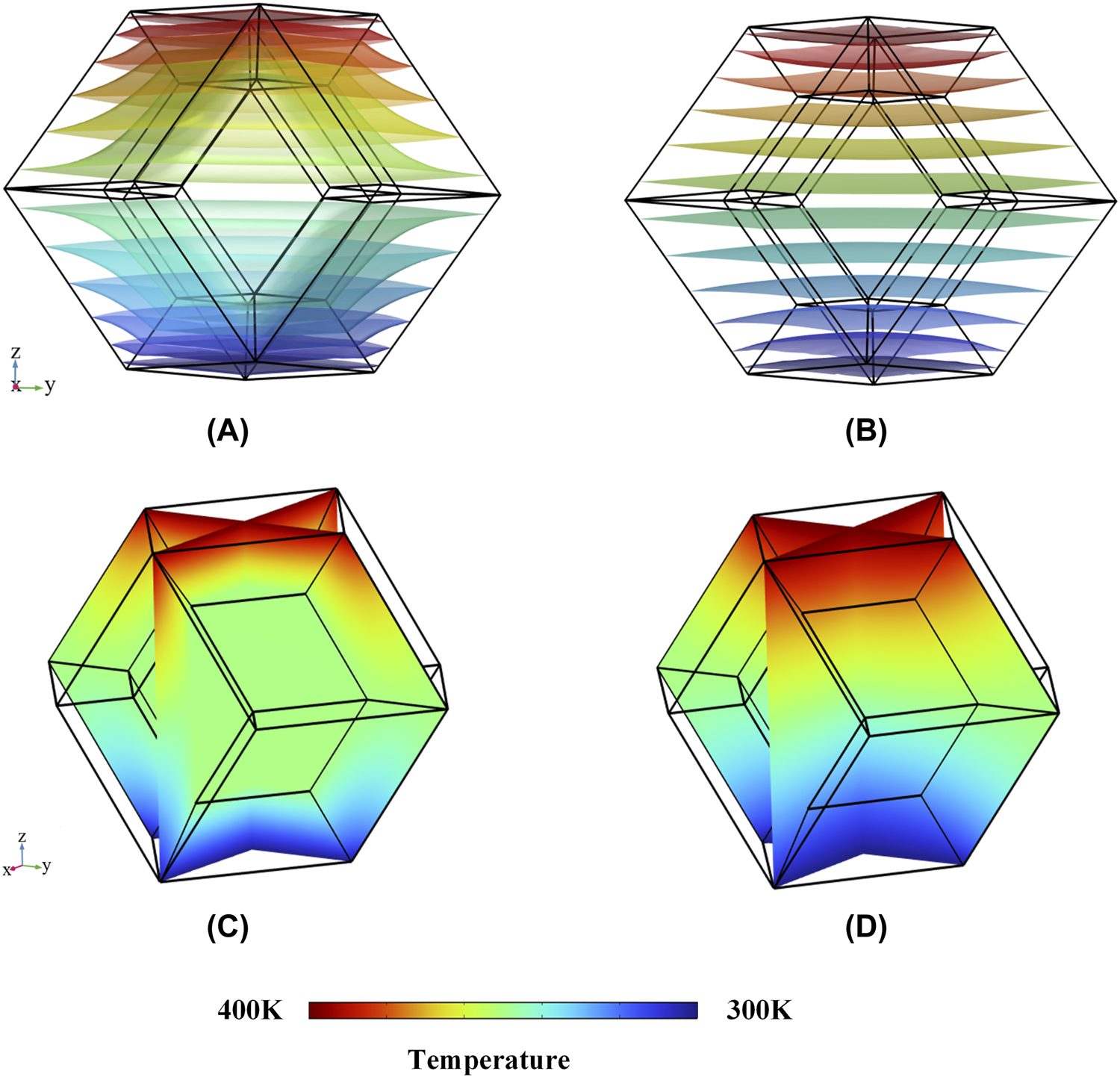
(A,B) The isothermal surface distribution of the rhombic dodecahedron with the thermal cloak effect or not. (C,D) Temperature distribution of the rhombic dodecahedron’s tangent plane with and without the cloak effect.
FIGURE 11
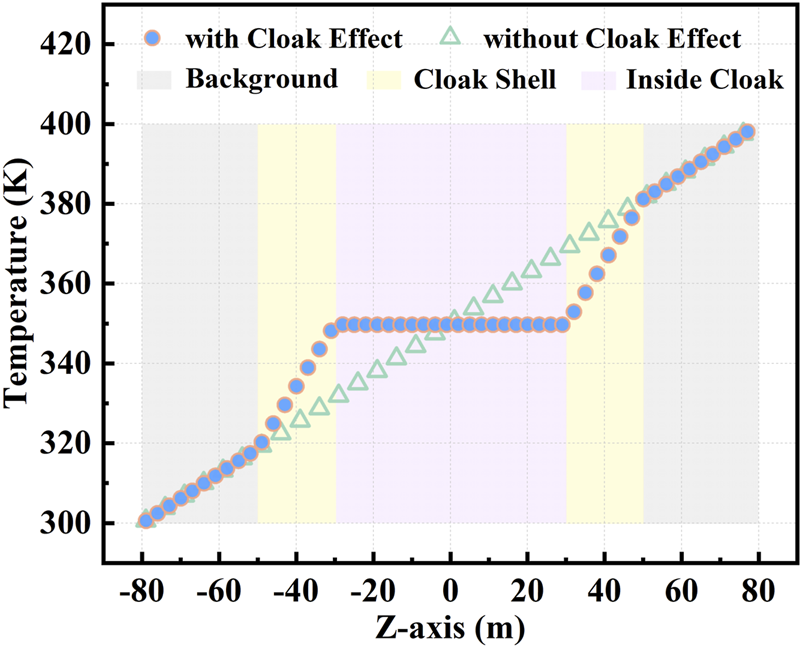
The temperature distribution on the center line of the background and the rhombic dodecahedron with and without the thermal cloak effect.
Conclusion and Perspectives
In summary, the thermal conductivity tensors of hexagonal and dodecahedral thermal invisibility cloaks are derived in this work. The numerical verification shows that both hexagonal and dodecahedral thermal invisibility cloaks can avoid heat flow, and the temperature gradient in their thermal invisibility region is zero. This proves the correctness of the derivation method and the thermal conductivity tensors calculated and lays the foundation for adjusting thermal fields with complex structures.
3D morphologic mechanical metamaterials with specific functions have extraordinary properties due to their 3D building blocks. Researchers have been studying exotic static mechanical properties such as stiffness and strength close to theoretical limits [25], high mechanical elasticity or energy absorption [35–37] or negative Poisson ratios [38, 39]. However, the mechanical properties of the combination with the thermal field are still limited. The thermal conductivity tensors of hexagonal and dodecahedral thermal cloaks calculated in this paper aim to provide a uniform temperature field for the applications and prevent the mechanical properties from being affected by the non-uniform stress and deformation caused by the heat flow in the actual work. Furthermore, geometric configurations and deformation effects may change the thermal pathway [40–42], which could provide an effective way to adjust the anisotropic thermal conductivities of the thermal cloak.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
YS conducted major research work and wrote this paper. JQ contributed to calculation and participated in the discussion of the research. YC and XY directed and participated in the discussion and analysis of the research work. YL directed the overall research work and guided the writing of the thesis. All authors contributed to the article and approved the submitted version.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the National Science Foundation of China (Grant No. 52192633).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
References
1.
Yang S Wang J Dai GL Yang F Huang J . Controlling Macroscopic Heat Transfer with Thermal Metamaterials: Theory, Experiment and Application. Phys Rep (2021) 908:1–65. 10.1016/j.physrep.2020.12.006
2.
Yang FB Zhang ZR Xu LJ Liu Z Jin P Zhuang P et al Controlling Mass and Energy Diffusion with Metamaterials. Rev Mod Phys (2024) 96:015002. 10.1103/RevModPhys.96.015002
3.
Zhang ZR Xu LJ Qu T Lei M Lin ZK Ouyang X et al Diffusion Metamaterials. Nat Rev Phys (2023) 5:218–35. 10.1038/s42254-023-00565-4
4.
Pendry JB Schurig D Smith DR . Controlling Electromagnetic Fields. Science (2006) 312:1780–2. 10.1126/science.1125907
5.
Fan CZ Gao Y Huang JP . Shaped Graded Materials with an Apparent Negative Thermal Conductivity. Appl Phys Lett (2008) 92:251907. 10.1063/1.2951600
6.
Narayana S Sato Y . Heat Flux Manipulation with Engineered Thermal Materials. Phys Rev Lett (2012) 108:214303. 10.1103/PhysRevLett.108.214303
7.
Li JY Gao Y Huang JP . A Bifunctional Cloak Using Transformation Media. J Appl Phys (2010) 108:074504. 10.1063/1.3490226
8.
Li Y Shen XY Wu ZH Huang J Chen Y Ni Y et al Temperature-Dependent Transformation Thermotics: From Switchable Thermal Cloaks to Macroscopic Thermal Diodes. Phys Rev Lett (2015) 115:195503. 10.1103/PhysRevLett.115.195503
9.
Schittny R Kadic M Guenneau S Wegener M . Experiments on Transformation Thermodynamics: Molding the Flow of Heat. Phys Rev Lett (2013) 110:195901. 10.1103/PhysRevLett.110.195901
10.
Zhang J Zhang HC Wang HM Xu C Wang Q . Performance Prediction of Nanoscale Thermal Cloak by Molecular Dynamics. Appl Phys A (2021) 127:790. 10.1007/s00339-021-04942-7
11.
Yang S Xu LJ Wang RZ Huang JP . Full Control of Heat Transfer in Single-Particle Structural Materials. Appl Phys Lett (2017) 111:121908. 10.1063/1.4994729
12.
Sha W Xiao M Zhang JH Ren X Zhu Z Zhang Y et al Robustly Printable Freeform Thermal Metamaterials. Nat Commun (2021) 12:7228. 10.1038/s41467-021-27543-7
13.
Ji QX Qi YC Liu CW Meng S Liang J Kadic M et al Design of Thermal Cloaks with Isotropic Materials Based on Machine Learning. Int J Heat Mass Tranfer (2022) 189:122716. 10.1016/j.ijheatmasstransfer.2022.122716
14.
Han TC Yang P Li Y Lei D Li B Hippalgaonkar K et al Full-parameter Omnidirectional Thermal Metadevices of Anisotropic Geometry. Adv Mater (2018) 30:1804019. 10.1002/adma.201804019
15.
Li WC Sigmund O Zhang XJS . Analytical Realization of Complex Thermal Meta-Devices. Nat Commun (2024) 15:5527. 10.1038/s41467-024-49630-1
16.
Xu L Dai G Yang F Liu J Zhou Y Wang J et al Free-form and Multi-Physical Metamaterials with Forward Conformality-Assisted Tracing. Nat Comput Sci (2024) 4:532–41. 10.1038/s43588-024-00660-1
17.
Hussein MI Tsai CN Honarvar H . Thermal Conductivity Reduction in a Nanophononic Metamaterial Versus a Nanophononic Crystal: A Review and Comparative Analysis. Adv Funct Mater (2020) 30:1906718. 10.1002/adfm.201906718
18.
Nutz FA Retsch M . Tailor-made Temperature-dependent Thermal Conductivity via Interparticle Constriction. Sci Adv (2017) 3:eaao5238. 10.1126/sciadv.aao5238
19.
Ren K Liu XJ Chen S Cheng Y Tang W Zhang G . Remarkable Reduction of Interfacial Thermal Resistance in Nanophononic Heterostructures. Adv Funct Mater (2020) 30:2004003. 10.1002/adfm.202004003
20.
Maire J Anufriev R Hori T Shiomi J Volz S Nomura M . Thermal Conductivity Reduction in Silicon Fishbone Nanowires. Scientific Rep (2018) 8:4452. 10.1038/s41598-018-22509-0
21.
Yan G Li Y Wang Y Yin G Yao S . Tunable Bandgap Characteristic of Various Hexagon-type Elastic Metamaterials for Broadband Vibration Attenuation. Aerospace Sci Technology (2024) 145:108872. 10.1016/j.ast.2024.108872
22.
Lu Z Yang YG Huang JL . Dual‐band Terahertz Metamaterial Absorber Using Hexagon Graphene Structure. Microwave Opt Technology Lett (2021) 63:1797–802. 10.1002/mop.32816
23.
Xu W Xiao X Chen J Han Z Wei K . Program Multi-Directional Thermal Expansion in a Series of Bending Dominated Mechanical Metamaterials. Thin-Walled Structures (2022) 174:109147. 10.1016/j.tws.2022.109147
24.
Torquato S Jiao Y . Dense Packings of the Platonic and Archimedean Solids. Nature (2009) 460:876–9. 10.1038/nature08239
25.
Kai Y Dhulipala S Sun R Lem J DeLima W Pezeril T et al Dynamic Diagnosis of Metamaterials through Laser-Induced Vibrational Signatures. Nature (2023) 623:514–21. 10.1038/s41586-023-06652-x
26.
De Jonge C Kolken H Zadpoor A . Non-auxetic Mechanical Metamaterials. Materials (2019) 12:635. 10.3390/ma12040635
27.
Cao X Duan S Liang J Wen W Fang D . Mechanical Properties of an Improved 3D-Printed Rhombic Dodecahedron Stainless Steel Lattice Structure of Variable Cross Section. Int J Mech Sci (2018) 145:53–63. 10.1016/j.ijmecsci.2018.07.006
28.
Prashanth K Löber L Klauss HJ Kühn U Eckert J . Characterization of 316L Steel Cellular Dodecahedron Structures Produced by Selective Laser Melting. Technologies (2016) 4:34. 10.3390/technologies4040034
29.
Yue XZ Matsuo K Kitazono K . Compressive Behavior of Open-Cell Titanium Foams with Different Unit Cell Geometries. Mater Trans (2017) 58:1587–92. 10.2320/matertrans.L-M2017834
30.
Cao X Ren X Zhao T Li Y Xiao D Fang D . Numerical and Theoretical Analysis of the Dynamic Mechanical Behaviour of a Modified Rhombic Dodecahedron Lattice Structure. Int J Mech Mater Des (2020) 17:271–83. 10.1007/s10999-020-09517-7
31.
Yang L Harrysson O West H Cormier D . Modeling of Uniaxial Compression in a 3D Periodic Re-entrant Lattice Structure. J Mater Sci (2012) 48:1413–22. 10.1007/s10853-012-6892-2
32.
Yu G Xiao L Song W . Deep Learning-Based Heterogeneous Strategy for Customizing Responses of Lattice Structures. Int J Mech Sci (2022) 229:107531. 10.1016/j.ijmecsci.2022.107531
33.
Milton GW Briane M Willis JR . On Cloaking for Elasticity and Physical Equations with a Transformation Invariant Form. New J Phys (2006) 8:248. 10.1088/1367-2630/8/10/248
34.
Huang JP . Theoretical Thermotics: Transformation Thermotics and Extended Theories for Thermal Metamaterials. Singapore: Springer Nature Singapore Pte Ltd (2020). p. 10.
35.
Meza LR Zelhofer AJ Clarke N Mateos AJ Kochmann DM Greer JR . Resilient 3D Hierarchical Architected Metamaterials. Proc Natl Acad Sci (2015) 112:11502–7. 10.1073/pnas.1509120112
36.
Portela CM Vidyasagar A Krödel S Weissenbach T Yee DW Greer JR et al Extreme Mechanical Resilience of Self-Assembled Nanolabyrinthine Materials. Proc Natl Acad Sci (2020) 117:5686–93. 10.1073/pnas.1916817117
37.
Guell IA Bauer J Crook C Turlo V Valdevit L . Ultrahigh Energy Absorption Multifunctional Spinodal Nanoarchitectures. Small (2019) 15:1903834. 10.1002/smll.201903834
38.
Babaee S Shim J Weaver JC Chen ER Patel N Bertoldi K . 3D Soft Metamaterials with Negative Poisson’s Ratio. Adv Mater (2013) 25:5044–9. 10.1002/adma.201301986
39.
Farzaneh A Pawar N Portela CM Hopkins JB . Sequential Metamaterials with Alternating Poisson’s Ratios. Nat Commun (2022) 13:1041. 10.1038/s41467-022-28696-9
40.
Bartlett MD Fassler A Kazem N Markvicka EJ Mandal P Majidi C . Stretchable, High-K Dielectric Elastomers through Liquid-Metal Inclusions. Adv Mater (2016) 28:3726–31. 10.1002/adma.201506243
41.
Zhang F Feng YY Qin MM Gao L Li Z Zhao F et al Stress Controllability in Thermal and Electrical Conductivity of 3D Elastic Graphene-Crosslinked Carbon Nanotube Sponge/polyimide Nanocomposite. Adv Funct Mater (2019) 29:1901383. 10.1002/adfm.201901383
42.
Yang L Yue SY Tao Y Qiao S Li H Dai Z et al Suppressed Thermal Transport in Silicon Nanoribbons by Inhomogeneous Strain. Nature (2024) 629:1021–6. 10.1038/s41586-024-07390-4
Summary
Keywords
thermal cloak, thermal metamaterials, coordinate transformation, hexagon, dodecahedron
Citation
Sun Y, Qi J, Chai Y, Yang X and Li Y (2025) Study on Thermal Cloaks for Hexagon and Dodecahedron With Symmetry. Aerosp. Res. Commun. 3:14950. doi: 10.3389/arc.2025.14950
Received
24 May 2025
Accepted
05 September 2025
Published
02 October 2025
Volume
3 - 2025
Updates
Copyright
© 2025 Sun, Qi, Chai, Yang and Li.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yueming Li, liyueming@mail.xjtu.edu.cn
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.